Задания математической олимпиады 5, 6 и 7 классы

На данной страницы размещены олимпиадные задания с решением для 5-7 класса.
Олимпиада по математике прошла 14 января 2018 года

Cкачать задание в формате Pdf

Посмотреть ответы на все задания олимпиады

Вторая Олимпиада, 14.01.2018

Задача №1

Разделите фигуру по линиям сетки на 5 равных частей. В каждой части должна быть ровно одна звёздочка и ровно один шестиугольник.

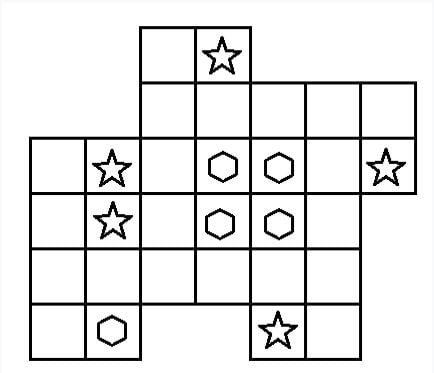
Задача №2

Антон, Боря, Вася, Гога и Даня встали в ряд. Подпишите имя каждого мальчика, если известно, что:

Антон не с краю.
Боря в очках.
Вася не кудрявый.
Гога без очков.
Даня носит шорты в горошек.
Если Вася с краю, то Даня самый высокий.
Даня не кудрявый.

Задача №3

Ника рисует клеточные фигурки, в каждой следующей увеличивая и высоту, и ширину на 2 клетки (см. рисунок). А сколько клеток в такой же фигурке, высота которой 2017? Напишите ответ и решение.

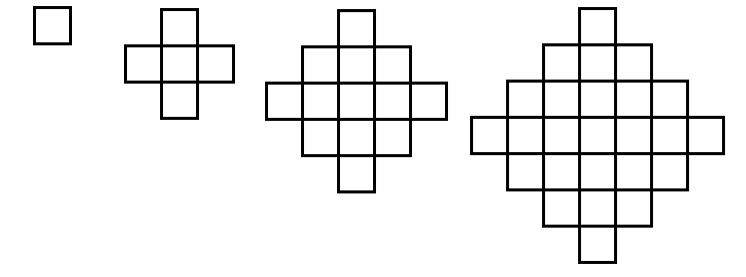
Задача №4

Можно ли расставить в вершинах кубика числа от 1 до 8 так, чтобы для каждой из шести граней сумма четырёх чисел в её вершинах была одной и той же. Если можно, приведите пример. Если нельзя, объясните почему.

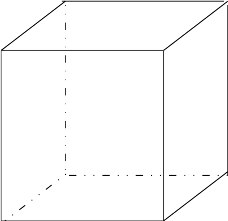
Задача №5

В море живут 6 мальков , 4 медузы, 3 осьминога и 1 акула. Море заколдовали, и теперь если медуза съест малька, то превратится в осьминога, а если осьминог съест малька, то превратится в акулу. Через год в море не осталось ни одного малька. Сколько осталось медуз, если акул стало 5? Напишите ответ и решение.

Задача №6

На чёрно-белую вечеринку пришли ребята или в полностью чёрном костюме, или в полностью белом. Когда в финальном танце все встали в круг и взялись за руки, то выяснилось, что:

тех, кто держат за руку мальчика и девочку — 20 человек;
тех, кто держат за руку двух девочек — 15 человек;
тех, кто держат за руку людей в костюмах разного цвета — 14 человек;
тех, кто держат за руку только людей в белом — 13 человек.

Кого на вечеринке больше: мальчиков или тех, кто в чёрном? На сколько?

Напишите ответ и решение.

Задача №7

В группе кружка 12 человек. Каждый из ребят подарил по одной открытке каждому своему другу. Оказалось, что подарено ровно 70 открыток. Потом на кружке стало слишком шумно и преподаватель рассадил ребят по двум аудиториям так, что в каждой из них не оказалось ни одной пары друзей. По сколько человек в каждой аудитории? Напишите ответ и решение.

Задача №8

Какое наименьшее значение может принимать сумма трёх слагаемых, если известно, что она должна делиться на 5, и при этом в записи слагаемых должны быть использованы все цифры? Напишите ответ и решение.