Разбор заданий конкурса Кенгуру по математике. 18 марта 2021. 6 класс
Решения:
Задача 1
Правильный ответ: Г
Ориентируемся на белые кирпичи, их дано два. Выбираем из предложенных конструкций ту, в которой два белых кирпича. Такая только одна – это конструкция Г.
Задача 2
Правильный ответ: А
Рассматриваем каждого ребенка. Чтобы держать друг друга за левые руки, дети должны стоять лицом в противоположные стороны. Таких пар три. При этом две из них держатся за правые руки, и только одна пара (пятая девочка и шестой мальчик) держат друг друга левыми руками.
Задача 3
Правильный ответ: Б
Сложив паззл, получим пример: 12+20. Ответ 32.
Задача 4
Правильный ответ: Б
Ворота состоят из 3 клеток, т.е. сквозь них сможет пройти только та фигура, которая в каждом горизонтальном ряду содержит не более 3 клеток. Все фигуры кроме В имеют ряды, в которых больше 3 клеток.
Задача 5
Правильный ответ: В
Перемножаем числа: 5, 10, 15, 20, … , 100. Среди них есть 10 чисел с нулями, которые при умножении дадут 11 нулей. Остаётся перемножить их же, но без нулей, и числа, оканчивающиеся на 5. То есть, умножаем: 1, 2, 3, 4, 5, 6, 7, 8, 9. Далее: 5, 15, 25, 35, 45, 55, 65, 75, 85, 95. Нас интересует, сколько двоек содержит первое произведение, так как, чтобы получить 0 при умножении числа, оканчивающегося на 5, достаточно его умножить на 2. Считаем количество двоек в первом произведении: 2, 4=2х2, 6=2х3, 8=2х2х2, их 7. Чисел с пятерками на конце больше, поэтому нулей при умножении будет столько же, сколько есть двоек в первом произведении, то есть 7. Добавляем эти 7 нулей к ранее полученным 11-ти, и получаем, что всего будет 18 нулей.
Задача 6
Правильный ответ: Г
Это квадрат Г. Он разделен на 4 части, а потом четверть разделена пополам.
Задача 7
Правильный ответ: Г
Начинаем с третьей коробки, там одна буква N. Её и берем. Далее из первой коробки берем Е, из пятой – U. Тогда из четвертой коробки останется взять G.
Задача 8
Правильный ответ: Д
Подходят все три фигуры. Прямоугольник складываем сначала вертикально посередине, потом по диагонали, квадрат – сначала по диагонали, потом пополам, треугольник – два раза пополам.

Решения:
Задача 9
Правильный ответ: Б
Разрезаем так, чтобы в результате получить наименьшие числа. Число содержит 10 цифр, значит, без четырехзначного числа не обойтись. Выбираем самое маленькое четырехзначное число, которое можно выделить из цифр предложенного числа, – это 1972, тогда трехзначные – это 502 и 970. Их сумма: 1972+502+970=3444.
Есть вариант выбрать два четырехзначных и одно двузначное числа, но их сумма окажется больше, чем 3444.
Задача 10
Правильный ответ: Б
Складывая числа 10, 15, 12, 13, получим длину маршрута «А – зоопарк – В – парк – С – порт – А» и удвоенную длину маршрута 15 км. Эта длина 10+15+12+13=50 км. Тогда искомый маршрут будет иметь длину, равную: 50–15∙2=20 км
Задача 11
Правильный ответ: А
Считаем, что А – вершина пирамиды. Второй слой – это шарики с буквами В, С, Е. Третий слой – шарики с буквами Д, ?, Е, С, Д, В. Поскольку по условию каждая буква написана на двух шариках, тогда на шарике со знаком вопроса написана буква А.
Задача 12
Правильный ответ: В
Каждая цифра замка повернута на одинаковое расстояние в одном и том же направлении, поэтому цифры шифра отличаются от чисел комбинации 6348 на одно и тоже число с учетом перехода через 0. Проверяем каждый вариант по очереди: в варианте А все цифры увеличены на 2, в Б – все уменьшены на 3, в варианте В – сбой: первая цифра уменьшена на 2, а вторая – на 4, поэтому варианта В не может быть.
Задача 13
Правильный ответ: Г
Пусть Влад взял х яблок, тогда груш он взял 20–х. Луке осталось 20–х яблок и х груш. Верно утверждение Г.
Задача 14
Правильный ответ: Б
Заметим, что скорость поезда из X в Y (назовем его первый ) в 3 раза меньше, чем скорость поезда из Y в X (назовем его второй). За одно и то же время второй поезд пройдет в 3 раза большее расстояние, чем первый. В сумме они пройдут 4 перегона. Всего от X до Y – 6 перегонов. 6÷4=1,5. Т.е. они встретятся на середине второго перегона, считая от X. На втором перегоне и нужно строить второй путь.
Задача 15
Правильный ответ: Б
Посчитаем сумму чисел в пустых кружочках. 30–(3+6+1+2)=18 – это сумма чисел в пустых кружочках левого шестиугольника. 30–(4+6+9+4)=7 – это сумма чисел в пустых кружочках правого шестиугольника. Посчитаем для среднего шестиугольника: 30–18–7–1=4 – число, стоящее в кружочке со знаком вопроса.
Задача 16
Правильный ответ: В
Найдем высоту прямоугольника. Она находится через прямоугольник со стороной AB. (12+18)÷6=5 см. Дальше рассмотрим прямоугольник со стороной CD и найдем его длину. (18+22) ÷5=8 см. Таким образом длина CD – 8 см.

Решения:
Задача 17
Правильный ответ: А
У маленькой шестеренки 10 зубчиков, а у больших по 13. При полном обороте маленькой шестеренки все шестеренки прокрутятся на 10 зубчиков. Ориентируемся по закрашенному зубчику, учитывая направление движения шестеренок. Маленькая крутится по часовой стрелке, большая нижняя будет крутиться против часовой стрелки, а большая справа – по часовой стрелке. Значит после полного оборота маленькой шестеренки они займут положение А.
Задача 18
Правильный ответ: В
Имеем:
Яблоко + Апельсин = Груша + Персик
Яблоко + Груша < Апельсин + Персик
Груша + Апельсин < Яблоко + Персик
Из первых двух соотношений следует, что 2 яблока весят меньше 2 персиков, то есть персик тяжелее яблока. Из первого и третьего соотношения следует, что 2 апельсина весят меньше 2 персиков, то есть персик тяжелее апельсина. Тогда из первого соотношения следует, что груша весит меньше яблока. Значит самый тяжелый – персик.
Задача 19
Правильный ответ: Д
Квадрат имеет 4 оси симметрии: вертикальную и горизонтальную посередине и две диагональные. Для симметрии относительно вертикальной оси дорисовываем такую же фигуру из 3 клеток. Получится фигура из 6 клеток. Тогда, рисуя симметрию относительно других трех осей заштриховываем 3∙6=18 клеток. Ответ 18+3=21.
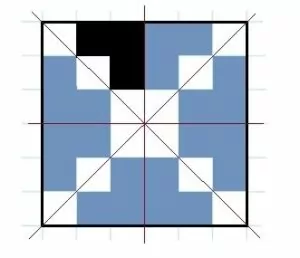
Задача 20
Правильный ответ: Б
Кубики с красной линией будут расположены в вершинах куба, их 8, и на диагоналях у шести квадратов (сторон куба) без учета крайних. На одной диагонали без крайних (они будут вершинами куба, уже их подсчитали) 7–2=5. На двух: 5∙2–1=9 – количество кубиков с красной чертой на одной стороне куба без тех, что расположены на краях. Вычитаем 1, так как 1 кубик будет общим для обеих диагоналей. Считаем: 8+9∙6=62.
Задача 21
Правильный ответ: Б
Если бы все сказали правду, то полученная сумма равнялась бы 55 (1+2+…+10=55). На самом деле она получилась меньше на 19 (55–36=19). Поскольку все числа лежат в промежутке от 1 до 10, то один тролль не мог уменьшить сумму на 19. Два тролля тоже не смогли бы уменьшить сумму на 19, потому что тогда одному из них нужно было бы уменьшить число на жетоне на 10, что невозможно. А вот три тролля могут уменьшить сумму на 19. Значит наименьшее количество троллей – 3.
Задача 22
Правильный ответ: Д
Обратим внимание на утверждение, что карты могут располагаться рядом только в том случае, если оба символа по общему краю будут совпадать. При этом на каждой карте все четыре символа различны, значит, чтобы их можно было использовать в формировании прямоугольника, последовательность символов должна быть определенной. На исходной карте по меньшей располагаются круг и звезда, а также треугольник и квадрат, а по большей – круг и треугольник, и звезда и квадрат. Это означает, что какие бы карты мы ни подбирали, символы на боковых сторонах заранее определены. Для горизонтального ряда подойдут карты с треугольником и квадратом по меньшей стороне – это карты Б и Г, а для вертикального – со звездой и квадратом по большей стороне – это карты А и В. Оставшаяся карта – Д – не будет использоваться при создании прямоугольника.
Задача 23
Правильный ответ: Г
Обозначим большую бутылку как «б», среднюю как «с», маленькую как «м». Имеем:
1 полка: 3б + 4м = 64
2 полка: 3м + 2б + 2с = 64
3 полка: 6м + 4с = 64.
Сравнивая 1 и 2 полки, замечаем, что 1б + 1м = 2с.
Заменяя на первой полке 3б + 3м на 6с, получим: 6с + 1м = 64, то есть 1м = 64 – 6с.
6м на третьей полке заменяем на 6∙(64 – 6с), и получим: 6∙(64 – 6с) + 4с = 64.
Решаем это уравнение. Получаем, что 1 средняя бутылка имеет объем 10 децилитров.
Задача 24
Правильный ответ: В
Анализируем ответы. Если предположить, что первый пират ответил правильно на первый вопрос, а на второй – неправильно, тогда получится, что второй пират неправильно ответил на первый вопрос, а правильно – на второй.
