Разбор заданий конкурса Кенгуру по математике. 18 марта 2021. 9 класс

Решения:

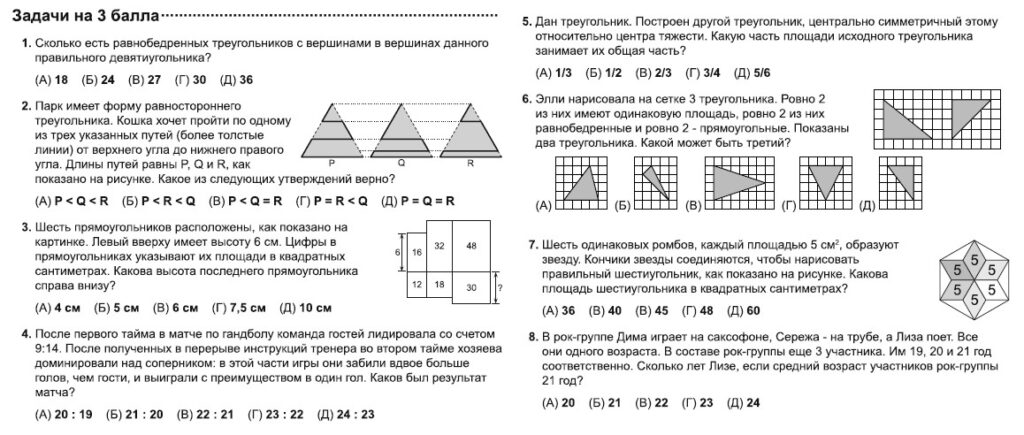
Задача 1
Правильный ответ: Г

Подсчитаем для каждой вершины число треугольников равнобедренных, но не правильных. Его вершина, в которой сходятся две равные стороны, является вершиной для трех таких треугольников. И так как всего вершин 9, то получаем 3∙9=27 равнобедренных треугольников. Кроме того, в девятиугольник можно вписать еще 3 различных правильных треугольника. Всего же будет 27+3=30.

Задача 2
Правильный ответ: Б

Сравниваем пути. У всех – одинаково нижнее основание и боковая сторона. Разница – в путях внутри треугольника. Получится самый маленький P, длиннее его путь R, самый длинный – Q.

Задача 3
Правильный ответ: Б

Рассматривая рисунок, замечаем прямоугольник, у которого известны две характеристики: площадь и длина стороны. Находим другую его сторону: 16÷6=8/3. Эта сторона общая с прямоугольником, площадью 12. Отсюда находим вторую сторону этого прямоугольника: 12÷8/3=9/2. Действуем так же с каждым последующим прямоугольником. Получаем: 18÷9/2=4, 32÷4=8, 48÷8=6, 30÷6=5 – это высота последнего прямоугольника

Задача 4
Правильный ответ: Б

Пусть во втором тайме гости забили х голов, тогда хозяева забили 2х голов. Получаем уравнение: 14+х+1=9+2х, Получаем, что х=6. Т.е. гости забили всего 14+6=20 голов, а хозяева 9+6∙2=21 гол. Значит, игра закончилась со счетом 20:21.

Задача 5
Правильный ответ: В

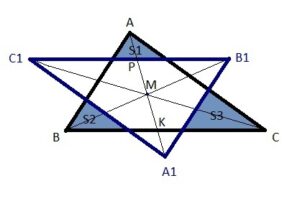
Центр тяжести треугольника (центроид) – это точка пересечения медиан, которая делит каждую медиану в отношении 2:1, считая от вершины. Чтобы получить вершины симметричного треугольника, медиану продлеваем от точки пересечения за сторону на такую же длину. Симметричные треугольники равны, соответствующие элементы в них тоже равны и симметричные стороны параллельны, поэтому отсеченные треугольники подобны данному с коэффициентом подобия 1/3.
Далее для наглядности см. рисунок в первом комментарии:
На рисунке ВС равна и параллельна С1В1, АМ =МА1, МК =А1К = 1/3(АК) = АР. Треугольник с площадью S1 подобен данному и его площадь равна 1/9 от площади данного. В сумме треугольники с площадями S1, S2, S3 будут иметь площадь, равную 1/3 площади данного. Тогда площадь общей части симметричных треугольников составляет от площади данного 2/3

Задача 6
Правильный ответ: Г

На рисунке показаны два прямоугольных треугольника с площадями 10 и 8 и один из них равнобедренный. Значит, третий треугольник равнобедренный, не прямоугольный с площадью 10 или 8. Подходит только вариант Г.

Задача 7
Правильный ответ: В

В правильном шестиугольнике радиус – (большая диагональ ромба) равен стороне шестиугольника. Тогда площадь белых треугольников будет в 2 раза меньше площади ромба, т.е. 2,5 кв.см. Считаем: 5∙6+2,5∙6=45 кв.см.

Задача 8
Правильный ответ: В

Пусть Диме, Сереже и Лизе по х лет. Среднее арифметическое возраста всех участников группы -21 год. Тогда составляем уравнение: (3х+19+20+21)÷6=21. Решив это уравнение, получим: х=22.

Решения:

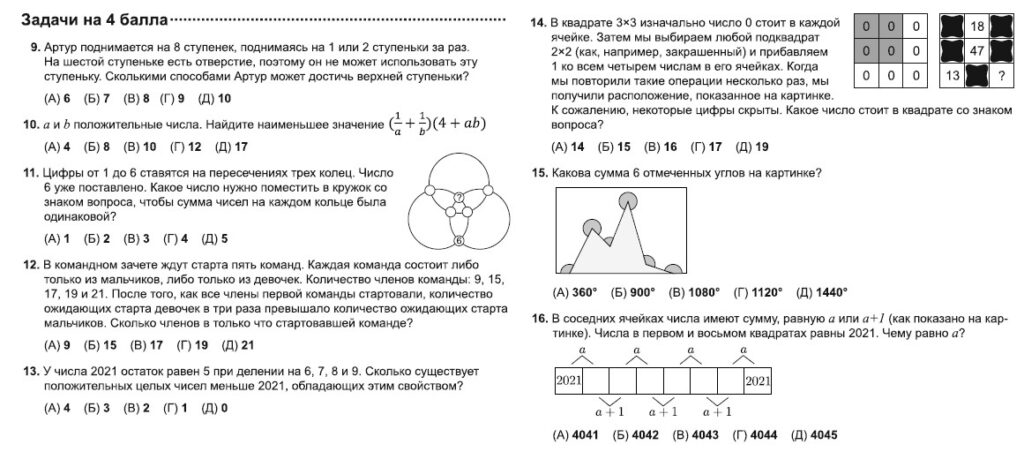
Задача 9
Правильный ответ: В

Исходная комбинация: 1,2,3,4,5,7,8. Подсчитываем все возможные комбинации, пропуская 1 или 2 числа. Таких комбинаций возможно 8.

Задача 10
Правильный ответ: Б

Применяем свойство: среднее арифметическое чисел больше или равно их среднему геометрическому.
(1/а + 1/b)∙( 4+аb) ≥ 2 √(1/аb)× √4аb = 8. Ответ 8

Задача 11
Правильный ответ: А
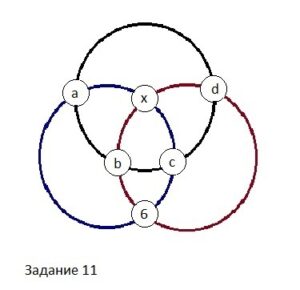
Обозначим числа в кружочках буквами (см. поясняющий рисунок в первом комментарии). Согласно условию получатся равенства: а+b+с+d=а+х+с+6=6+b+x+d.
Из первого и второго равенств следует, что b+d=х+6.
Из второго и третьего равенств получаем, что: а+с=b+d.
Сумма всех чисел в кружочках равна 1+2+3+4+5+6=21. Отсюда имеем уравнение: х+а+b+с+d+6=21.
Заменим в нем (b+d) и равное ему (а+с) на равное им (х+6).
Получим: 2(х+6)+х+6=21, откуда находим, что х=1.

Задача 12
Правильный ответ: Д

Подсчитаем количество всех детей, получится 9+15+17+19+21=81. Стартовала команда с х детьми. Количество оставшихся (81–х). Количество мальчиков (обозначим его у) среди оставшихся будет равно (81–х)÷ 4. Число у, как и число х принимает одно из значений количества членов команд — то есть одно из чисел: 9, 15, 17, 19, 21. Проверяем каждое и получаем, что подходит х=21.

Задача 13
Правильный ответ: А

Числа, обладающие этим свойством, образуют арифметическую прогрессию, уменьшающуюся на число, кратное указанным. Наименьшее положительное число, которое без остатка делится на 6, 7, 8 и 9 равно 7∙8∙9=504. Уменьшая последовательно число 2021 на 504, получим остальные числа, обладающие этим свойством: 1517, 1013, 509, 5. Итого — четыре числа.

Задача 14
Правильный ответ: В

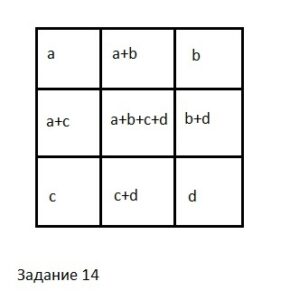
К нулям нижнего левого подквадрата 13 раз прибавляли 1. Тогда 47–13=34, это количество прибавлений 1 к нулям в правом и левом верхнем и правом нижнем подквадратах. В сумме в правом верхнем и левом верхнем прибавили 18 единиц, тогда в нижнем правом прибавили 34–18=16 единиц – это число, стоящее в квадратике со знаком вопроса.
Для наглядности см. рисунок в первом комментарии.

Задача 15
Правильный ответ: В

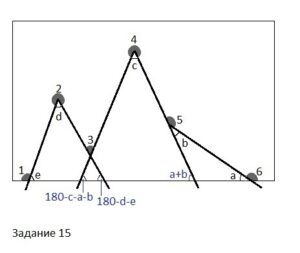
Проще решить эту задачу, обозначая углы разными буквами и выражая остальные через них. Для этого достроим фигуру, выделив треугольники, как на рисунке (см. рисунок в первом комментарии).
Обозначим некоторые углы а, b, с, d и e. Тогда сразу находим, что второй справа угол будет равен (a+b), третий справа – (180-d-e), а второй слева – (180-с-а-b). Они показаны на рисунке.
Угол 3 равен: 180-(180-d-e)-(180-с-a-b)=-180+d+e+с+a+b.
Сумма всех шести интересующих нас углов составит: (180-e)+(360-d)+(-180+d+e+с+a+b)+(360-c)+(180-b)+(180-a)=1080.

Задача 16
Правильный ответ: Д

Заполняя клеточки последовательно, получим, что в предпоследней правой клетке находится число 2024. Тогда а=2024+2021=4045

Решения:

Задача 17
Правильный ответ: В

Из первого равенства следует, что: (а+b)=-с, (b+с)=-а, (с+а)=-b. Умножая их, получим (-аbс)=-78.

Задача 18
Правильный ответ: А

Наименьшее число с конкретной суммой цифр будет содержать как можно меньше разрядов, и тогда, как можно больше девяток. 2021÷9=224 (остаток 5). Число N=599…9999. В нем 224 девятки. Прибавляем 2021, получим число 600….02020. Его сумма цифр — 10.

Задача 19
Правильный ответ: Д

Семен набрал 19 баллов, один из вариантов 19=6∙3+1, 3 слова в этом случае общие. Этот вариант не подходит, так как, в этом случае, максимальное число баллов у Артема равно 21, а у второго тогда должно быть 20, что невозможно. Это значит, что у Семена баллы получились 19=5∙3+4∙1+1∙0, тогда у каждого есть 1 одно общее слово. 4 слова по 1 очку он делит с двумя другими: 3 – со вторым мальчиком и 1 с Артемом. Баллы второго мальчика: 6∙3+3∙1+1∙0=21, баллы Артема: 8∙3+1∙1+1∙0=25.

Задача 20
Правильный ответ: Г

Пусть а=p^2, b=q^2. Тогда p^2–g^2=(p–q)∙(p+q) – простое число по условию. Простое число раскладывается только на два множителя: 1 и само себя. Тогда p-q=1 (т.к. оно точно меньшее из двух). Подбираем из предложенных:
Вариант А: q=10, тогда p=11, 10+11 – не простое, не подходит;
Вариант В: q= 12, тогда p=13, 12+13=25 – не подходит.
Перебирая таким образом все предложенные варианты, находим, что подойдет вариант Г.

Задача 21
Правильный ответ: Г

Будет рассматривать возможные варианты. Для наглядности они изображены на рисунке в первом комментарии.
Начнем с квадратика (1;1), тогда возможен единственный вариант раскраски, рисунок 1.
Теперь первым раскрасим квадратик (1 по горизонтали, 2 – по вертикали), в этом случае возможны два варианта раскраски остальных квадратов, рисунок 2.
Когда начнем раскраску с верхней правой клеточки, то в этом случае возможны 2 вида раскраски остальных квадратиков, рисунок 3.
Всего получается 5 разных вариантов.

Задача 22
Правильный ответ: В

Расположим числа, равные весу монет в порядке возрастания, пусть это ряд: а,b,с,d,е,f,g,h. По условию они все различны, наибольшее число обозначено буквой h. Нужно найти наименьшее значение, тогда а — тоже наименьшее и равно 1. 1+d> b+с, тогда наименьшее d =5. Далее, рассуждая аналогично, получим искомый ряд чисел: 1,2,3,5,8,13,21,34. Значит самая тяжелая монета весит 34 грамма.

Задача 23
Правильный ответ: Г

Среди любых пяти последовательных шаров есть один красный, один желтый, один синий и два зеленых. Сказанное выше справедливо как для первых пяти, так и для последних пяти шаров. Рассмотрим любые шесть последовательных шаров. Отсюда следует, что первый и шестой шары имеют одинаковый цвет. Следовательно, цвет любого шара повторяется после пяти последовательных шаров. Таким образом, шар с номером 20 имеет тот же цвет, что и шар с номером 5 (так как 20=5∙3+5). Шарик с номером 202 имеет тот же цвет, что и шарик с номером 2 (так как 202=5∙40+2). Таким образом, шары с номером 2 и с номером 5 — зеленые. Шар с номером 2021 имеет тот же цвет, что и шар с номером 1 (2021=5∙404+1). Отсюда следует, что шар номер 3 -красный, номер 4 — желтый и номер 1 — синий. Следовательно, шар с номером 2021 имеет синий цвет.

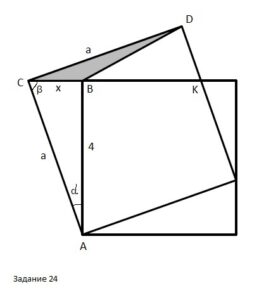
Задача 24
Правильный ответ: Б

Обозначим некоторые стороны и углы как на рисунке (см. рисунок в первом комментарии): АС=СD=a, CB=x, угол CAB = углу DCB =α, угол ВСА =β.
Площадь большого квадрата в этом случае будет a^2.
Видим, что треугольник АВС прямоугольный, тогда α=90-β.
Площадь треугольника СВD S=1=(1/2)ax∙sinα.
Из треугольника АВС находим sinα=х/а. Тогда 1=(1/2)ах(х/а). Отсюда получаем, что x^2=2.
Т.к. a^2=x^2+4^2, то находим, что a^2=2+16=18.