Задания 1-го тура XII олимпиады по математике для 1 класса

Гномик Силач рассматривал фотографии гномиков Отто и Порто. Сосчитайте, сколько всего отличий Силач увидел между гномиками Отто и Порто? Варианты ответа: (А) 4; (Б) 7; (В) 8; (Г) 5; (Д) 10.

Гномики Силач, Бородач, Тягач, Весельчак и Говорун пошли за покупками к Новому году. Они купили Ёлку, игрушки и сладости. Кто что нес, если Бородач и Говорун не несли ёлку, Силач и Тягач не несли игрушки, Весельчак не нёс ни елку, ни игрушки? Варианты ответа: (А) Силач и Бородач - елку, Тягач и Говорун - игрушки, Весельчак - сладости; (Б) Силач и Говорун - елку, Тягач и Бородач - игрушки, Весельчак - сладости; (В) Силач и Весельчак - елку, Говорун и Бородач - игрушки, Тягач - сладости; (Г) Бородач и Весельчак - елку, Говорун и Тягач - игрушки, Силач - сладости; (Д) Силач и Тягач - елку, Говорун и Бородач - игрушки, Весельчак - сладости.

По дороге из магазина гномики Силач, Бородач, Тягач, Весельчак и Говорун встретили Деда Мороза и загадали ему загадку: Силач говорит: «я родился первого числа второго месяца года. Бородач говорит: «я родился первого числа первого месяца зимы». Тягач говорит: «я родился первого сентября». Весельчак говорит: «я родился первого числа последнего месяца зимы». Говорун говорит: «я родился первого числа последнего месяца лета». Кто из них является близнецами? Варианты ответа: (А) Силач и Весельчак; (Б) Бородач и Тягач; (В) Силач и Тягач; (Г) Бородач и Говорун; (Д) Весельчак и Говорун.

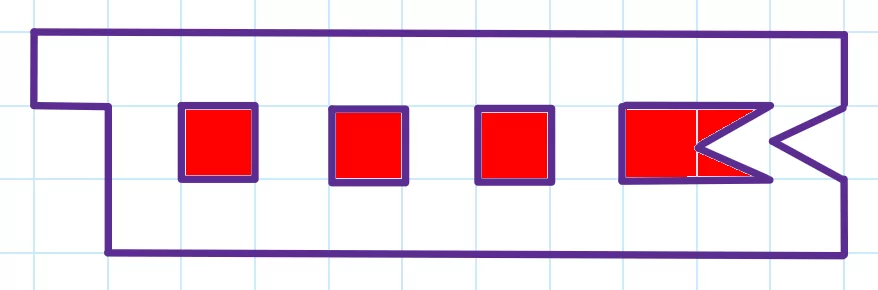
Гномики принесли Снегурочке кусок ткани и попросили вырезать слово так, чтобы обрезков не осталось. Снегурочка выполнила просьбу гномов, вырезала несколько букв и составила слово. Какое слово могло получиться у Снегурочки? (Красным цветом показаны пустые отверстия. Высота букв в слове по количеству клеток — одинаковая) Варианты ответа: (А) дом; (Б) рог; (В) зонт; (Г) гном; (Д) енот.

Гномики захотели узнать сколько лет Снегурочке? Она ответила: «Мне столько же сколько Весельчаку и Силачу вместе, возраст которых одинаковый. А возраст Весельчака равен половине возраста Говоруна, которому 8 лет». Варианты ответа: (А) 6; (Б) 8; (В) 12; (Г) 10; (Д) 4.

К новому году гномики купили 20 шариков на ёлку шести цветов: золотые, серебряные, розовые, синие, оранжевые и красные. Они развешивали их в таком порядке: Силач — золотой, Бородач — серебряный, Тягач — розовый, Весельчак — синий, Говорун — оранжевый, Силач — красный, Бородач — золотой, т. д. Кто повесит последний шарик и какого цвета? Варианты ответа: (А) Тягач — розовый; (Б) Говорун — золотой; (В) Силач — серебряный; (Г) Бородач — оранжевый; (Д) Говорун — серебряный.

Гномики Силач, Бородач, Тягач, Весельчак и Говорун имели хотя бы по одной игрушке. У двух гномиков было по одной пирамидке, у двух гномиков было по одной машинке, у трёх гномиков было по одному шарику. И не было ни одного гномика без игрушек. Сколько было гномов с двумя игрушками? Варианты ответа: (А) 1; (Б) 2; (В) 3; (Г) 4; (Д) 5.

В новогоднюю ночь в полночь Дед Мороз подарил гномикам волшебные часы. Каждые 60 мин часы бьют столько ударов, сколько времени на часах (1 час ночи — 1 удар, 2 часа ночи — 2 удара и т.д.) С каждым ударом из часов выпадают подарки в следующем порядке: носок — конфетка — шарик, так что 1 удар — 1 подарок. Сколько пар носков выпало из волшебных часов к моменту, когда часы закончили бить 4 часа утра в новогоднюю ночь? Варианты ответа: (А) 7; (Б) 4; (В) 6; (Г) 2; (Д) 5.

Сани Деда Мороза могут выдержать определённый вес подарков. Дед Мороз знает вес всех подарков кроме сапога. Найдите чему равен вес сапога, если все подарки весят одинаково и вес одного подарка равен — 2? Варианты ответа: (А) 10; (Б) 8; (В) 14; (Г) 12; (Д) 6.

Какое число обозначает мешок в ребусе: (А) 5 (Б) 10 (В) 15 (Г) 20 (Д) 25