Задания Одиннадцатой Олимпиады по математике Осень 2022 2 тур 8 класс

На данной страницы размещены олимпиадные задания с решением для 8 класса.
Олимпиада по математике прошла 23 октября 2022 года

Cкачать задание в формате PDF

Посмотреть ответы на все задания олимпиады

Задание №1

Квадрат числа , куб числа . Назовем «тетраэдром» натурального числа такое число, которое расположено ровно посередине между кубом и квадратом на числовой прямой. Докажите, что сумма первых 17 «тетраэдров» кратна 3.

Задание №2

Автор: Иванюк Дмитрий

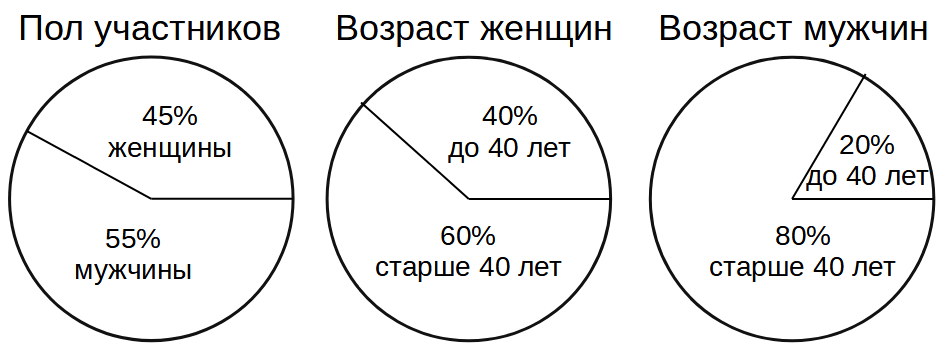
На приведенном ниже рисунке представлена информация о процентном составе (по группам) участников конкурса.

а) Всего было 360 женщин в возрасте 40 лет и младше. Подсчитайте количество мужчин в возрасте до 40 лет.

б) Рассчитайте процент всех участников старше 40 лет

Задание №3

Автор: Вольфсон Георгий

Найдите наименьшее четное натуральное число (целое положительное число), в записи которого единиц меньше, чем нулей, но больше, чем троек, а нулей меньше, чем пятерок. Не забудьте обосновать, почему указанное число — наименьшее!

Задание №4

Автор: Вольфсон Георгий

Петя, Коля и Вася бегали кросс. Вася бежал с постоянной скоростью. Петя первую половину пути бежал со скоростью, вдвое большей Васиной, а вторую половину — со скоростью, вдвое меньше Васиной. Коля же две трети пути бежал со скоростью, в пять раз больше Васиной, а последнюю треть — со скоростью, в три раза меньше Васиной. Кто из ребят прибежал первым?

Задание №5

Автор: Вольфсон Георгий

В прямоугольном треугольнике АВС с прямым углом С гипотенуза АВ = 20 см. Может ли его высота СН быть равной 15 см.

Задание №6

Автор: Вольфсон Георгий

Маша нарисовала квадрат по клеточкам. Катя вырезала из него другой квадрат по клеточкам. Могли ли при этом от машиного квадрата остаться невырезанными 30 клеточек?

Задание №7

Автор: Альперин Михаил Исаакович

ABC — равнобедренный прямоугольный треугольник. На продолжении катета AB за вершину B отложили отрезок BK, а на продолжении катета AC за вершину C — отрезок CL, причём BK=CL. На отрезке KL взяты точки E и F так, что BE⊥KC и AF⊥KC. Докажите, что EF=FL.

Задание №8

Автор: Иванюк Дмитрий

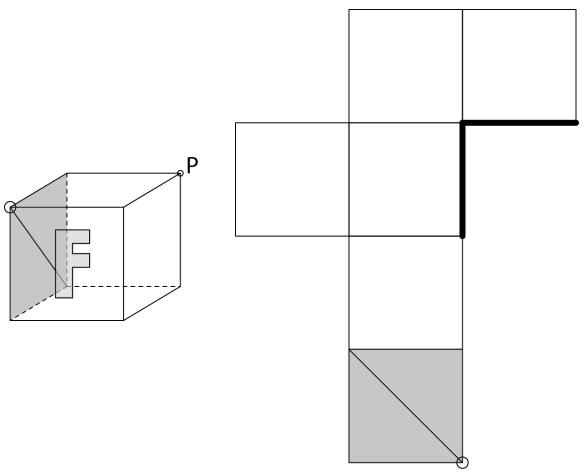
На передней грани куба (на рис. справа) расположена буква “F”. Куб расположили на плоскости и разрезали по рёбрам, получив его развёртку.

а) На модели куба нарисуйте ребро куба, выделенное жирным на его развёртке.

б) Нарисуйте угол P на развёртке.

в) Нарисуйте букву “F” на развёртке. Обратите внимание на правильное положение буквы “F”.