Задания Четырнадцатой Олимпиады по математике Осень 2023 2 тур 8 класс

Задача №1.
Автор: Тодоров Евгений

Яша и Зюзя изобрели свои температурные шкалы.
Яша принял за 0 температуру, при которой у него замерзает левая пятка, а 1 градус по его шкале — это то, насколько нагревается камешек, если Яша держит его в руке ровно минуту.
А Зюзя принял за 0 температуру, при которой он начинает шмыгать носом и чихать, а за 1 градус принимает то, как меняется температура железного шарика, если Зюзя дышит на него ровно минуту.
Каждый из изобретателей сделал термометр для своей шкалы и пошли мерить всё на свете. Оказалось, что если нагреть что-то на 1 градус по шкале Яши, то оно нагреется на 2 градуса по шкале Зюзи; а ещё оказалось, что 0 по шкале Зюзи равен 6 по шкале Яши.
Какая температура будет выражаться одинаковым числом градусов по обеим шкалам?

Задача №2.
Автор: Нилов

Даня написал на доске 4 различных натуральных числа. Федя для каждой пары чисел выписал отношение большего к меньшему (всего 6 чисел).
Сколько различных чисел могло получиться у Феди?
Для каждого варианта приведите пример 4 чисел и докажите, что других вариантов быть не может.

Задача №3.
Автор: Тодоров Евгений

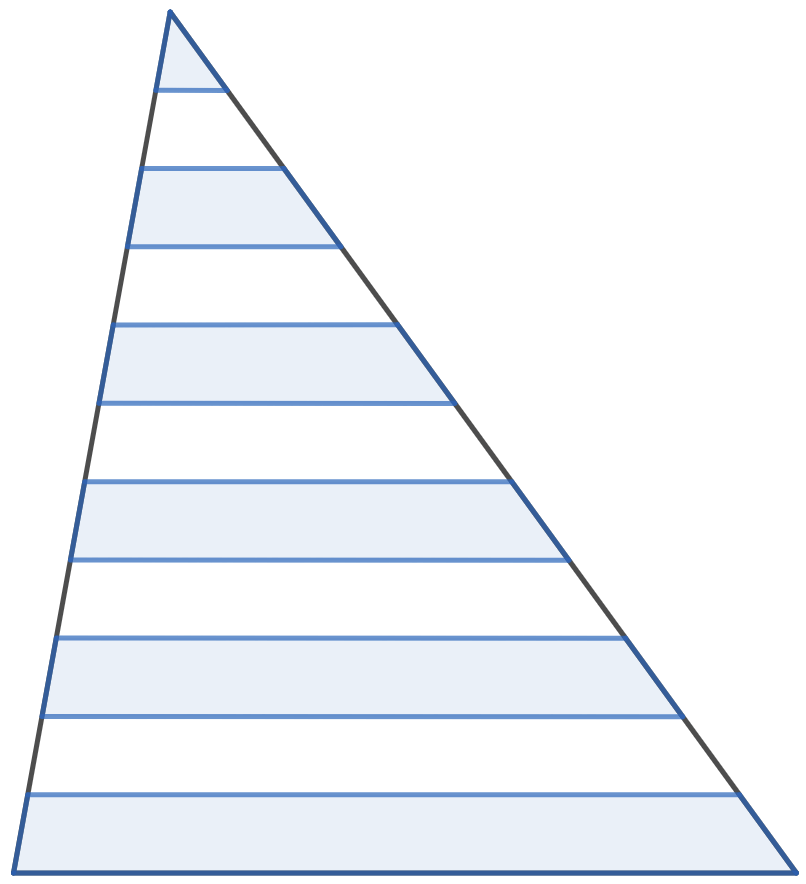
Произвольный треугольник разделён на 11 полосок одинаковой ширины, параллельных одной из сторон, как показано на рисунке. Известно, что суммарная площадь голубых полосок равна 330.
Чему равна площадь всего треугольника?

Задача №4.
Автор: Иванюк Дмитрий

Что больше 49! или (7!)⁸?
Пользоваться калькулятором для объяснения ответа не допустимо.

Задача №5
Автор: Тодоров Евгений

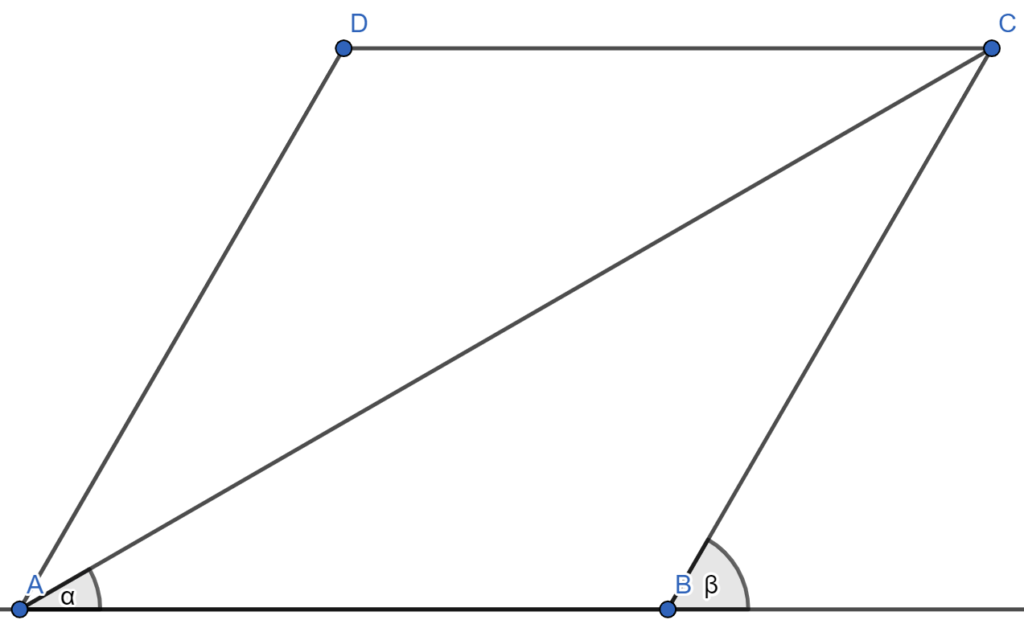
В параллелограмме ABCD сумма угла CAB и угла, смежного с ABC, равна 90°. Кроме того, известно, что AD = 10, а AC = 25. Найдите площадь параллелограмма.

Задача №6.
Автор: Тодоров Евгений

У гномов есть особенный праздник, который называется пятисумье. Это день рождения гнома, в который ему исполняется количество лет, в пять раз большее, чем сумма цифр его года рождения. Например, у гнома, родившегося в 2000 году пятисумье наступит в 10 лет, а у родившегося в 1999 — в 140 (отметим, что гномы живут очень долго). Гномы-математики Регин и Радсвинн, родившиеся в XX и XXI веке соответственно, вычислили, что их пятисумье наступит в один день.
Какой может быть разница в их возрастах?
Найдите все варианты ответа.

Задача №7.
Автор: Тодоров Евгений

Четверо рассеянных гномов нашли три двенадцатикилограммовых золотых самородка и хотят разделить их на троих так, чтобы каждый получил одинаковый суммарный вес золота. Для этого они разбивают самородки на куски и собирают свою долю из них. Известно, что если кому-то из рассеянных гномов попадётся кусок, весящий 3 килограмма или меньше, он обязательно потеряет его на обратном пути.
Докажите, что на обратном пути будет потерян хотя бы один кусок золота.

Задача №8.
Автор: Тодоров Евгений

Назовём число n суммоквадратовым, если существует табличка 2n, в первой строке которой записаны числа от 1 до n (каждое по одному разу в строке) в прямой последовательности, а во второй — в какой-то другой, а сумма в каждом столбике является квадратом некоторого натурального числа. Например, числа 3 и 5 являются суммоквадратовыми, потому что существуют таблицы

1 2 3
3 2 1

и

1 2 3 4 5
3 2 1 5 4,

в которых сумма в каждом столбике будет точным квадратом.
Докажите, что суммоквадратовых чисел бесконечно много.