Задания 1-го тура XV олимпиады по математике для 1 класса
1 тур XV олимпиады по математике прошел с 15 января по 6 февраля 2024 года.
Задачи олимпиады
Задача №1
На какое максимальное количество частей можно разделить звезду на картинке двумя прямыми?
(А) 3 (Б) 4 (В) 5 (Г) 6 (Д) 7

Галиулина В. Н.
Задача №2
У доктора Фасилье есть пара заколдованных кубиков, один – черного, другой – крас ного цвета. При броске одновременно красного и черного кубиков, сумма выпавших чисел на них всегда равна 7. Принц Навин подсчитал, что сумма всех выпавших чисел на красном кубике за три таких броска равна 9. Чему равна сумма чисел на черном кубике за эти же броски?
(А) 12 (Б) 11 (В) 10 (Г) 13 (Д) 5
Галиулина В. Н.
Задача №3
48 детей водили хоровод вокруг новогодней елки. При этом, каждый мальчик дер жал за руки двух девочек, а каждая девочка – девочку и мальчика. Сколько мальчиков было на празднике?
(А) 12 (Б) 16 (В) 20 (Г) 24 (Д) 32
Галиулина В. Н.
Задача №4
Аня выше Насти, а у Кати нет косичек. Можно ли определить, кто здесь Настя?
(А) Да, девочка 1 (Б) Да, девочка 2 (В) Да, девочка 3 (Г) Нет, точно определить нельзя
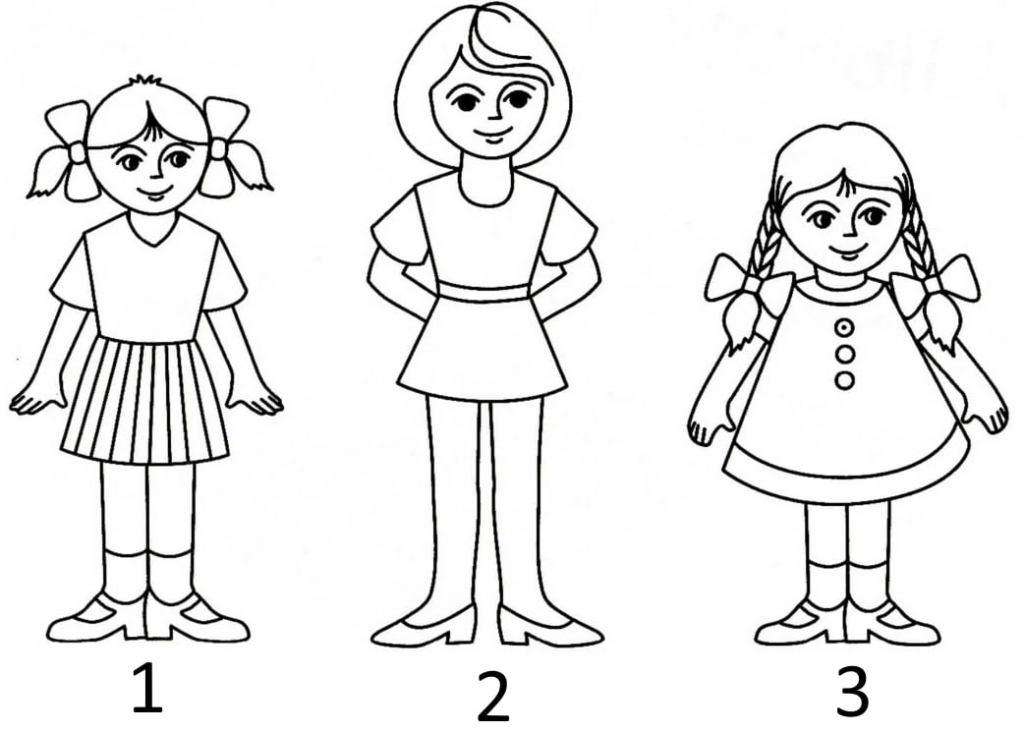
Галиулина В. Н.
Задача №5
Сколько пар сапог у марсианской кошки Марьяны, если на передних лапах 2 сапога, на задних лапах 2 сапога, на левых лапах 2 сапога, на правых лапах 2 сапога?
(А) 8 (Б) 4 (В) 2 (Г) 6 (Д) 3
Тодоров Е. И.
Задача №6
На картинке ниже цифрами обозначены люди: 1 — Егор; 2 — Лиза; 3 — Маша; 4 — Саша; 5 — Олег; 6 — Герман; 7 — Полина; 8 — Карина; 9 — Тимофей. Линии между цифрами показывают кто с кем дружит. Определите у кого больше всего друзей.
(А) у Саши (Б) у Маши (В) у Егора (Г) у Полины (Д) у Олега
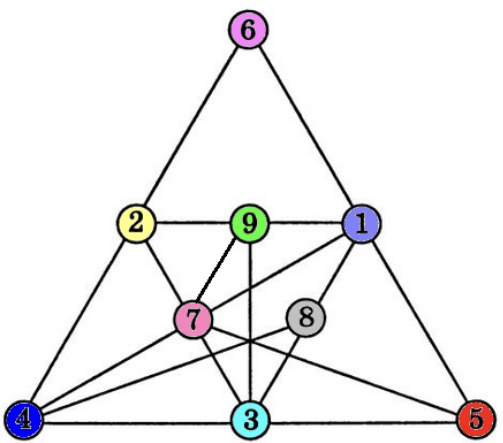
Тодоров Е. И.
Задача №7
Вероника собирала бусы в подарок и располагала бусины в следующем порядке: синяя круглая, красная розочка, 2 зелёных лепесточка, синяя круглая, красная розоч ка, и так далее. Сколько синих бусин Веронике потребовалось для бус, если послед няя бусина была синяя круглая и на бусы ушло 9 красных розочек?
(А) 9 (Б) 8 (В) 10 (Г) 11 (Д) 7
Иванюк Е. В.
Задача №8
Фермер купил Хрюнделя за 8 тугриков, продал его за 11, потом вновь купил того же Хрюн деля за 9 тугриков и опять продал, но уже за 10. Какую прибыль он получил за обе сделки?
(А) 2 тугрика (Б) 3 тугрика (В) 4 тугрика (Г) 5 тугриков
Галиулина В. Н.
Задача №9
Одинаковыми фигурами зашифрованы одинаковые цифры. Разными – разные. Ка кая цифра зашифрована оранжевым треугольником?
(А) 4 (Б) 5 (В) 6 (Г) 7 (Д) 8
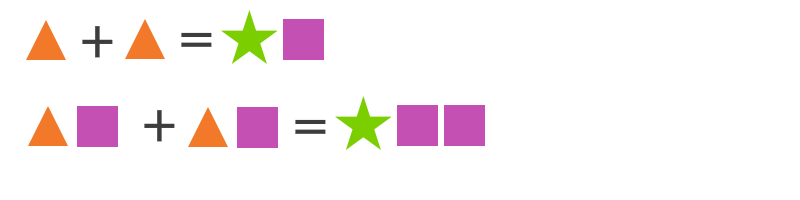
Галиулина В. Н.
Задача №10
Какое наименьшее количество веточек нужно отрезать, чтобы все красные ёлочные игрушки упали, а все шары остались?
(А) 3 (Б) 4 (В) 5 (Г) 6 (Д) 7

Галиулина В. Н.
| Задача № | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Ответ | Г | А | Б | В | В | Г | В | В | Б | Г |
I тур: 15 сентября - 27 сентября 2026
II тур: 25 октября 2026
Олимпиада по математике
Двадцать первая международная
Участвуйте в очередной математической олимпиаде от Систематики! Олимпиада проходит в два тура, по итогам которых победители получают ценные призы грамоты и дипломы.
Регистрация участника
Бесплатно


