Задания 1-го тура XIХ олимпиады по математике для 9 класса
1 тур XIХ олимпиады по математике прошел с 15 по 29 сентября 2025 г.
Задачи олимпиады
Задача №1
Три окружности с радиусами 2, 3 и 3 касаются друг друга. Какова площадь треугольника, образованного соединением центров этих окружностей?
A)10 Б)12 В)14 Г)16
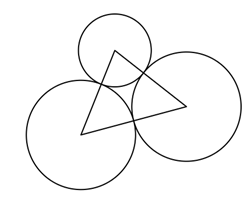
Варвара Галиулина
Задача №2
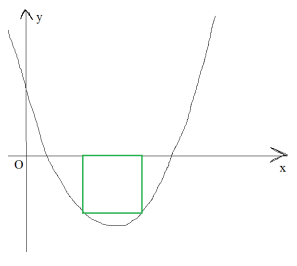
В сегмент, который отсекает прямая y=0 от параболы y = x² - 6x + 2, вписан квадрат (см. рисунок). Две вершины квадрата лежат на оси x. Чему равна сторона квадрата? Выберите значение, которое наиболее близко к правильному ответу.
(A) 3,5 (Б) 3,7 (В) 3,9 (Г) 4,0 (Д) 4,2
Михаил Евдокимов
Задача №3
Сколькими способами числа от 1 до 10 (разумеется, взятые по одному разу) можно разбить на пять пар так, чтобы в каждой паре меньшее число было хотя бы вдвое меньше большего?
А) 10 Б) 12 В) 32 Г) 24
Евгений Тодоров
Задача №4
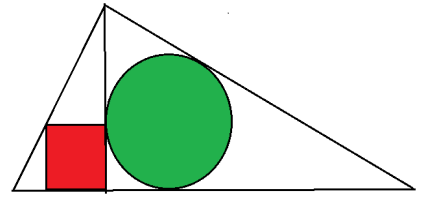
В прямоугольном треугольнике ABC с прямым углом C проведена высота CH. Радиус круга и сторона квадрата, вписанных в образовавшиеся треугольники равны 1 (см. рисунок). Чему равна гипотенуза AB? Ответ округлите до десятых.
А) 6.2 Б) 6.3 В) 6.4 Г) 6.5 Д) 6.6
Задача №5
При составлении автомобильных номеров в России используется следующее правило: в начале идёт одна заглавная буква, далее три цифры (скажем, что возможны абсолютно любые комбинации, даже три нуля). После чего идут две заглавные буквы и номер региона (сегодня это нам не понадобится). Назовём "красивыми" такие номера, где одинаковы либо все буквы, либо все цифры, либо и то, и другое сразу. Какое количество комбинаций "красивых" номеров может существовать? Буквы, которые можно использовать при составлении номера представлены ниже (после олимпиады можете подумать, почему только эти буквы можно использовать): А, В, Е, К, М, Н, О, Р, С, Т, У, Х.
А) 29160 Б) 17280 В) 12000 Г) 35780
Задача №6
В начале учебного года Вася пишет вступительную контрольную работу по математике. Вероятность того, что ему попадется лёгкий вариант равна $0.3$, вариант средней степени сложности — $0.5$, и самый маловероятный исходит приходится на "выпадание" сложного варианта — $0.2$. Вероятность того, что Вася справится с легким вариантом равна $0.6$, со средним — $0.4$, а силы Васи решить самый сложный вариант оцениваются в $0.2$. Какова вероятность того, что Вася успешно напишет контрольную работу?
А) 0.15 Б) 0.25 В) 0.32 Г) 0.42
Задача №7
Снята с зачета
Задача №8
Упростите выражение. Чему будет равен свободный коэффициент у получившегося многочлена?
а) 1 б) 2 в) 3 г) 4
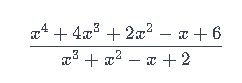
Данил Миронов
Задача №9
В квартире Сидоровых живут папа, мама и несколько детей. Месяц назад папе исполнилось 46 лет. Сегодня, когда вся семья соберётся за столом, среднее арифметическое их возрастов будет равно 22. Но через пару дней папа уедет в рабочую командировку, и когда мама и дети будут ужинать, среднее арифметическое их возрастов будет равно 18. Сколько детей в семье Сидоровых?
А) 4 Б) 5 В) 6 Г) 7
Евгений Тодоров
| Задача № | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Ответ | Б | Б | Б | Б | А | Г | – | В | Б |
I тур: 15 сентября - 27 сентября 2026
II тур: 25 октября 2026
Олимпиада по математике
Двадцать первая международная
Участвуйте в очередной математической олимпиаде от Систематики! Олимпиада проходит в два тура, по итогам которых победители получают ценные призы грамоты и дипломы.
Регистрация участника
Бесплатно



