Задания 1-го тура XХ олимпиады по математике для 3 класса
1 тур XIХ олимпиады по математике прошел с 13 января по 2 февраля 2026 г.
Задачи олимпиады
Задача №1
На рынке "Пират-мармелад" можно взять 1 ириску и 1 шоколадку и обменять их на 7 карамелек. А 1 шоколадку можно обменять на 2 ириски и 1 карамельку. Сколько ирисок можно обменять на 10 карамелек?
А) 2 Б) 4 В) 5 Г) 6 Д) 7

Дарья Шаинская
Задача №2
Даша задумала двузначное число, сумма цифр которого равна 15. Если поменять цифры этого числа, получится число на 9 меньше задуманного. Какое число задумала Даша?
А) 69 Б) 96 В) 78 Г) 87
Дарья Шаинская
Задача №3
София раскладывает шарики на полки определённым образом, как показано на рисунке. Как будет выглядеть ряд шариков на последней полке?
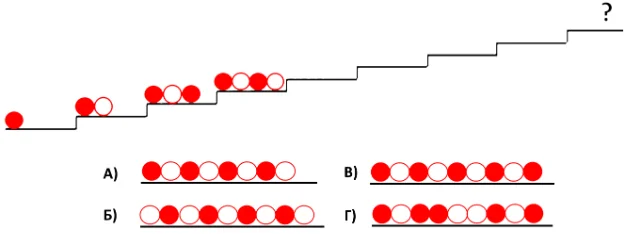
Варвара Галиулина
Задача №4
Сколько разных маршрутов есть у короля, при условии, что он может идти только по направлению стрелок?
А) 8 Б) 2 В) 3 Г) 7 Д) 12 Е) 24

Варвара Галиулина
Задача №5
Катя нарезала колбасу и хочет разложить ее на порезанный батон хлеба. Если на каждый кусок хлеба она положит по 2 кусочка колбасы, бутербродов получится на 2 больше, чем если она положит по три кусочка колбасы на каждый кусок хлеба. Сколько кусков колбасы нарезала Катя?
А) 8 Б) 10 В) 12 Г) 14 Д) 16
Дарья Шаинская
Задача №6
Ваня составил параллелепипед (если посмотреть на него спереди, сверху, и слева, увидим прямоугольник) из одинакового количества белых и серых кубиков (как показано на рисунке). Сколько белых кубиков не видно?
А) 4 Б) 6 В) 8 Г) 2

Варвара Галиулина
Задача №7
В круг встали 2025 ребят. Оказалось, что напротив каждого мальчика стоят две девочки. Какое наибольшее количество мальчиков могло стоять в кругу?
А)675 Б)1012 В)1013 Г)2023
Варвара Галиулина
Задача №8
В мини-отеле были только трехместные и двухместные номера. Всего отель мог принять 41 посетителя. Но позже половину двухместных номеров переделали в трехместные, и теперь в отеле могли проживать уже 46 человек. Сколько всего номеров было в отеле?
А) 15 Б) 17 В) 19 Г) 21 Д) 23

Дарья Шаинская
Задача №9
Маша собрала фигуру из 10 одинаковых пятиугольников с цифрами от 1 до 5. Детали соединялись так, чтобы стороны с одинаковыми числами соприкасались, как показано на рисунке с четырьмя видимыми деталями.
А) 1 Б) 2 В) 3 Г) 4 Д) 5
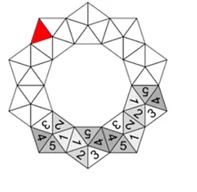
Варвара Галиулина
| Задача № | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Ответ | В | Г | В | Г | В | Г | Б | Б | А |
I тур: 15 сентября - 27 сентября 2026
II тур: 25 октября 2026
Олимпиада по математике
Двадцать первая международная
Участвуйте в очередной математической олимпиаде от Систематики! Олимпиада проходит в два тура, по итогам которых победители получают ценные призы грамоты и дипломы.
Регистрация участника
Бесплатно


