Задания 1-го тура XХ олимпиады по математике для 5 класса
1 тур XХ олимпиады по математике прошел с 13 января по 2 февраля 2026 г.
Задачи олимпиады
Задача №1
Какое время показывают часы, если после того как часовая стрелка указывала ровно на 8, минутная стрелка повернулась на пять прямых углов по часовой стрелке?
А) 8:15 Б) 9:00 В) 9:15 Г) 10:30 Д) 11:00 Е) 12:00
Варвара Галиулина
Задача №2
Иван Денисович написал на доске 8 последовательных натуральных чисел. Затем он закрыл некоторые числа треугольниками, некоторые — квадратами, а одно число — кругом. Сумма чисел под треугольниками равна сумме чисел под квадратами, а число под кругом составляет четверть этой суммы. Какое число скрыто под кругом, если известно, что общая сумма всех чисел меньше 100?
А) 8 Б) 6 В) 9 Г) 4 Д) 7 Е) 5
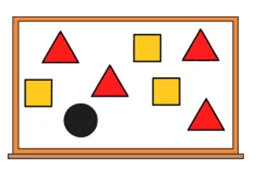
Варвара Галиулина
Задача №3
Кирилл загадал трехзначное число, а Даша попыталась его угадать, высказав предположения: Число делится на 9. Число больше 295. Число делится на 4. Число нечетное. Сумма цифр числа равна 15. Число меньше 300. Оказалось, что Даша ошиблась только в двух своих предположениях. Какое число загадал Кирилл?
А) 296 Б) 297 В) 298 Г) 299
Дарья Шаинская
Задача №4
Магазин «Кактус и Ко» работает с 11:20 утра до 21:30 вечера. В воскресенье он закрывается на час раньше. Еще у кактусов есть перерыв с 15:00 до 15:40 по будням и с 15:00 до 16:00 по выходным. По вторникам магазин закрыт — в этот день кактусы пересчитывают свои иголки. Сколько часов в неделю работает магазин?
А) 55 часов 40 минут Б) 55 часов 20 минут В) 56 часов 20 минут Г) 60 часов

Варвара Галиулина
Задача №5
Андрей гулял по лесной просеке, двигаясь по прямой. Если бы он шел с привычной скоростью, он бы прошел просеку за 30 минут. Но каждый раз, пройдя 100 метров, он останавливался на минуту, чтобы срезать увиденный гриб (причём на самых краях просеки грибы не растут). И прогулка заняла у него 49 минут. Какова привычная скорость Андрея?
А) 4 км/ч Б) 6 км/ч В) 5 км/ч Г) 3 км/ч
Дарья Шаинская
Задача №6
Снята с зачета
Задача №7
В классе десять человек. Известно, что если взять в группу шесть любых учеников, то каждого из оставшихся будет знать хотя бы один человек из группы. Какое наименьшее число знакомств может быть в таком классе?
А) 9 Б) 10 В) 20 Г) 45
Варвара Галиулина
Задача №8
Умник загадал три последовательных натуральных числа. Первое он умножил на два, второе – на три, третье – на шесть, после чего все результаты произведений сложил. Какое из перечисленных чисел у него не могло получиться?
А) 26 Б) 125 В) 245 Г) 356
Варвара Галиулина
Задача №9
Снята с зачета
| Задача № | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Ответ | В | Г | Б | Б | А | – | В | В | – |
I тур: 15 сентября - 27 сентября 2026
II тур: 25 октября 2026
Олимпиада по математике
Двадцать первая международная
Участвуйте в очередной математической олимпиаде от Систематики! Олимпиада проходит в два тура, по итогам которых победители получают ценные призы грамоты и дипломы.
Регистрация участника
Бесплатно


