Задания 1-го тура XХ олимпиады по математике для 6 класса

Сколько раз цифра 0 встречается в записи всех чисел от 1 до 2026 включительно?

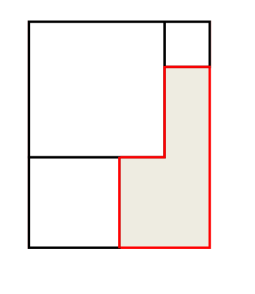
Из прямоугольника вырезали три квадрата так, как показано на рисунке. Сторона меньшего квадрата в 2 раза меньше стороны среднего квадрата и в 3 раза меньше большего квадрата. Во сколько раз периметр фигуры, оставшейся после вырезания квадратов, меньше периметра исходного прямоугольника?

В скольких четырёхзначных числах все цифры одинаковой чётности?

Сумасшедший изобретатель приделал к часам ещё одну дополнительную стрелку, которая вращается равномерно против часовой стрелки. В полдень часовая, минутная и дополнительная стояли на отметке 12. После чего дополнительная стрелка впервые встретилась с минутной в 12:45. В какое время дополнительная стрелка впервые встретится с часовой?

В вазе лежат конфеты - шоколадные, мятные и апельсиновые. Если вытащить наугад любые 12 конфет, среди них обязательно будет одна апельсиновая, если вытащить наугад любые 9 - среди них обязательно будет мятная, а если вытащить любые 10 - обязательно будет шоколадная. Какое наибольшее число конфет могло быть в вазе?

Андрей гулял по лесной просеке, двигаясь по прямой. Если бы он шел с привычной скоростью, он бы прошел просеку за 30 минут. Но каждый раз, пройдя 100 метров, он останавливался на минуту, чтобы срезать увиденный гриб (причём на самых краях просеки грибы не растут). И прогулка заняла у него 49 минут. Какова привычная скорость Андрея?

Кирилл загадал трехзначное число, а Даша попыталась его угадать, высказав предположения: Число делится на 9. Число больше 295. Число делится на 4. Число нечетное. Сумма цифр числа равна 15 Число меньше 300. Оказалось, что Даша ошиблась только в двух своих предположениях. Какое число загадал Кирилл?

Умник загадал три последовательных натуральных числа. Первое он умножил на два, второе – на три, третье – на шесть, после чего все результаты произведений сложил. Какое из перечисленных чисел у него не могло получиться?

Шестизначное число, состоящее из цифр 1, 2, 3, 4, 5 и 6 назовём красивым, если при прочтении числа слева направо выполнены следующие условия: цифра 2 идёт после цифры 1, но перед цифрой 3; цифра 5 идёт после цифры 6, но перед цифрой 4. Например, число 612534 будет красивым, потому что оба условия выше выполняются. Сколько существует красивых шестизначных чисел?