Задания 1-го тура XХ олимпиады по математике для 7 класса

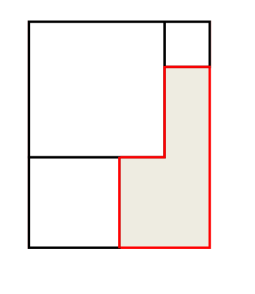
Из прямоугольника вырезали три квадрата так, как показано на рисунке. Сторона меньшего квадрата в 2 раза меньше стороны среднего квадрата и в 3 раза меньше большего квадрата. Во сколько раз периметр фигуры, оставшейся после вырезания квадратов, меньше периметра исходного прямоугольника?

Сумасшедший изобретатель приделал к часам ещё одну дополнительную стрелку, которая вращается равномерно против часовой стрелки. В полдень часовая, минутная и дополнительная стояли на отметке 12. После чего дополнительная стрелка впервые встретилась с минутной в 12:45. В какое время дополнительная стрелка впервые встретится с часовой?

В ромбе ABCD угол A равен 74 градуса. На диагонали AC взяли точку K такую, что AK = BK + CK. Найдите угол KBC.

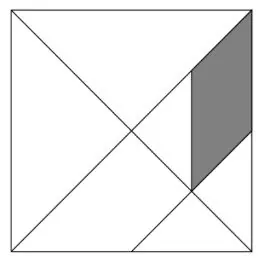
Фигура ниже изображена абсолютно точно. Каждая точка серой фигуры совпадает либо с вершиной квадрата, либо с серединой какого-то из отрезков, проведенных в квадрате. Если площадь большого квадрата равна 128 см2 , то чему равна площадь серой фигуры?

Пусть N это произведение 20 сомножителей 1!·2!·3!·…·20!, где n! = 1·2·3·…·n – произведение целых чисел от 1 до n. На какое наименьшее натуральное число нужно домножить N, чтобы получился полный квадрат?

В вазе лежат конфеты - шоколадные, мятные и апельсиновые. Если вытащить наугад любые 12 конфет, среди них обязательно будет одна апельсиновая, если вытащить наугад любые 9 - среди них обязательно будет мятная, а если вытащить любые 10 - обязательно будет шоколадная. Какое наибольшее число конфет могло быть в вазе?

Сколько существует равнобедренных треугольников с целыми длинами сторон и периметром 2026?

Математик Илюша решил придумать свою, математическую новогоднюю ёлку, поэтому он написал на доске цифры 2, 0, 2 и 6, а числа в каждой следующей строчке получал по следующему принципу: - в начале всегда 2; - в конце всегда 6; - все промежуточные числа равны сумме верхнего левого и верхнего правого их соседей. Первые четыре строчки новогодней ёлки Илюши выглядят так (см. рисунок) Сумма всех чисел в последней поместившейся на доску строчке равна 5120. Чему равно предпоследнее число в этой строчке?