Пробная олимпиада

Пройдите пробную олимпиаду по математике для 1–9 классов.
IV олимпиада по математике прошла 27 января 2019 года.
Задача №1
Разделите закрашенную фигуру на три равные части.
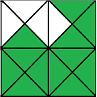
Задача №2
Странный лифт открыл двери на 1 этаже, затем на 4, затем на 7, 10 и так далее, он ехал вверх и открывал двери через каждые три этажа. В небоскрёбе 87 этажей. На каком этаже лифт открыл двери в последний раз?
Задача №3
Муравей ползает по проволочному октаэдру. Сможет ли муравей проползти по всем рёбрам (сторонам) октаэдра ровно по одному разу? Если может, нарисуйте его путь.
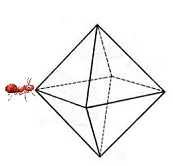
Задача №4
Ника взяла два картонных шестиугольника и положила их рядом друг с другом. Какое наименьшее количество углов могло получиться у получившейся фигуры? Нарисуйте картинку, как Ника могла сложить шестиугольники.
Задача №5
Ася, Тася и Вася любят разные конфеты: шоколадные, мармеладные и вафельные. «Я люблю шоколадные» - сказала Ася. «Я не люблю мармеладные» - сказала Тася. Кто любит какие конфеты, если обе девочки соврали?
Задача №6
Кот ходит по роялю. Сначала он шагнул на клавишу номер 1, затем на клавишу 2, затем на клавишу 4. Так каждый следующий номер был в два раза больше чем предыдущий. Когда кот не может сделать ход по этим правилам, он спрыгивает на пол. Оказалось, что у рояля 88 клавиш. Какой номер у последней клавиши, которую посетил кот?
Ответы на задачи №1-6 в формате разборов
1-й тур: 23 сентября — 6 октября
2-й тур: 27 октября
Олимпиада по математике
ШЕСТНАДЦАТАЯ МЕЖДУНАРОДНАЯ ОЛИМПИАДА СИСТЕМАТИКИ
Участвуйте в очередной математической олимпиаде от Систематики! Олимпиада проходит в два тура, по итогам которых победители получают ценные призы грамоты и дипломы.
Зарегистрироваться
Бесплатно



