Задания Двенадцатой Олимпиады по математике Зима 2023 2 тур 1 класс

Задача №1.

Автор: Мартешева Анастасия

Маша пересчитывает лепестки по кругу. Пятый лепесток оказался оранжевым.
С каких лепестков могла начать счёт Маша?

Задача №2.

Автор: Санкеева Ольга

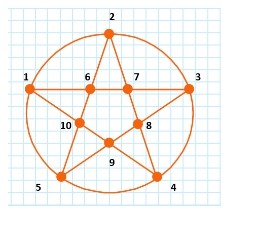
Укажите путь по точкам, по которому можно нарисовать данную фигуру, не отрывая ручки от листа и не проводя дважды по одной и той же линии. В ответе укажите номера точек, по которым нужно нарисовать путь.
Можно начинать путь с любой точки.

Задача №3.

Автор: Ольга МК

Для изготовления зелья ведьме нужно 26 ингредиентов. 5 из них съедобные продукты, остальные ядовитые или травы. Ядовитых ингредиентов было 8, из них травами были 3.
Сколько всего видов трав нужно ведьме?

Задача №4.

Автор: Варданян Амаяк

Мальчика Тома попросили присмотреть за овцами и курами во дворе. Да вот беда! Ему сообщили, что всего у животных 11 головы и 28 ног.
Сколько овец и кур было?

Задача №5

Автор: Санкеева Ольга

Ева играет в палочки. Она собрала из 13 палочек фигуру (смотрите рисунок). Какие 6 палочек Еве нужно переложить, чтобы получить 4 квадрата?

Задача №6.

Автор: Санкеева Ольга

Помогите Элли вернуться домой обратно в Канзас. Чтобы преодолеть горы, девочке нужно сделать 7 шагов в волшебных башмачках.
Сколько раз Элли коснётся земли за весь путь, когда приземлится в родном крае? Сколько времени займет дорога у Элли, если на 1 шаг уходит 4 минуты и в каждой точке нужно сделать остановку на 1 минуту для толчка? (Точку отсчета движения и точку приземления тоже посчитать как касание и остановку).

Задача №7.

Автор: Санкеева Ольга

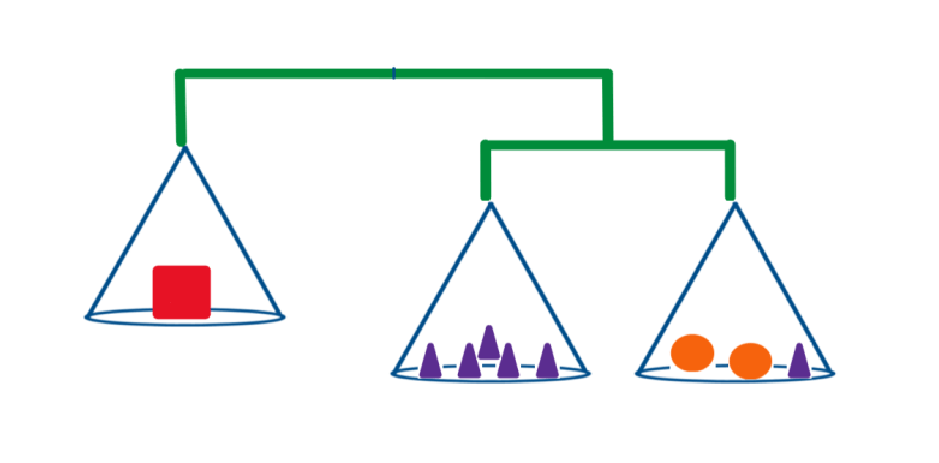
Масса квадрата равна 6 треугольникам и 2 кругам, массы одинаковых по форме фигур равны. Посмотрите на рисунок и определите скольким кругам равна масса квадрата.
(Примечание: Считать массу самой конструкции равной 0)

Задача №8.

Автор: Гавва Анна

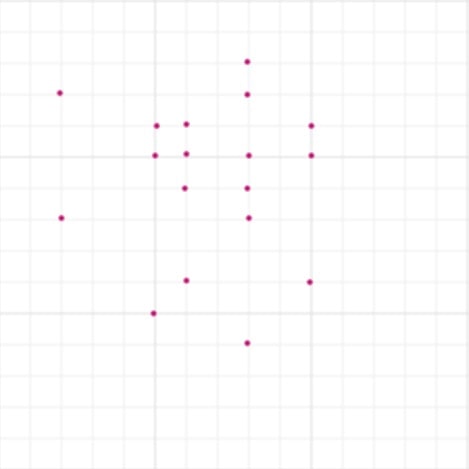
Соедините точки, чтобы получилось наибольшее количество квадратов. Каждая точка может быть вершиной нескольких квадратов и может лежать на стороне другого. Сколько квадратов у вас получилось?
(Стороны квадратов могут пересекаться)