Задания 1-го тура XIV олимпиады по математике для 1 класса
1 тур XIV олимпиады по математике прошел с 18 по 30 сентября 2023 года.
Задачи олимпиады
Задача №1
Бабушка с дедушкой шли из леса домой. На встречу им шла соседка Люба с внучкой. Сколько человек шли домой? (А) 0 (Б) 2 (В) 3 (Г) 4
Гавва А. С.
Задача №2
Белоснежка купила стулья для семи гномов. У некоторых стульев было три ножки, а у других четыре. Ножек всего оказалось 14. Сколько стульев ещё нужно купить, чтобы всем (вместе с Белоснежкой) хватило места? (А) 2 (Б) 3 (В) 4 (Г) 5
Гавва А. С.
Задача №3
Таня играет в классики. Она может прыгать в соседнюю по стороне клетку и по диагонали. Прыжок по диагонали называется «длинным», прыжок в соседнюю клетку – «коротким». Таня хочет пропрыгать так, чтобы получить слово СИСТЕМАТИКА. Насколько длинных прыжков она сделает меньше, чем коротких? (А) 4 (Б) 6 (В) 7 (Г) 3

Галиулина В. Н.
Задача №4
Бабушка поставила на стол тарелку с конфетами. К тарелке подбежали внуки и забрали оттуда по одной конфете, после чего конфет в тарелке стало 14. На следующий день бабушка поставила на стол такую же тарелку с конфетами, как и в прошлый день. К тарелке вновь прибежали внуки, но на этот раз они положили в тарелку по конфете, и конфет стало 22. Сколько внуков у бабушки? (А) 8 (Б) 4 (В) 2 (Г) 6
Тодоров Е. И.
Задача №5
У кота Леопольда в гараже лежал запутанный клубок веревок. После того, как он связал какие-то четыре пары веревок между собой и пересчитал концы, концов оказалось 14 штук. Сколько веревок лежало в шкафу изначально? (А) 7 (Б) 9 (В) 11 (Г) 13
Галиулина В. Н.
Задача №6
Некоторые кочки на болоте в лягушачьей деревне соединены мостиками. Лягушонок Прутик вылез из болота на ближайшую кочку, прошелся по трем разным мостикам и очутился на кочке под номером один. На какую кочку Прутик не мог вылезти изначально? (А) 1 (Б) 2 (В) 3 (Г) 5
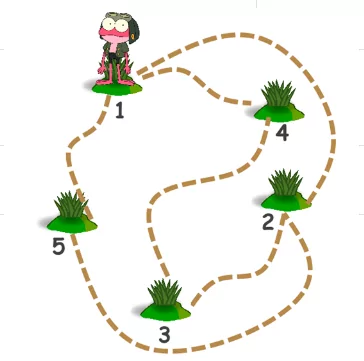
Галиулина В. Н.
Задача №7
Уиллис Дэвидж учит маленького инопланетянина Заммиса считать на пальцах до десяти. Они начинают считать одновременно. Когда пальцы у кого-то на левой руке заканчиваются, он начинает загибать на правой. Когда пальцы и на правой руке заканчиваются, он разгибает все пальцы и начинает загибать сначала. Сколько пальцев загнул Заммис в тот момент, когда у Дэвиджа было загнуто 4 пальца на правой руке, если у Заммиса на каждой руке всего по 4 пальца (руки у инопланетянина тоже две)? (А) 0 (Б) 1 (В) 2 (Г) 3
Галиулина В. Н.
Задача №8
В деревне лягушек, в пункте обмена можно получить: 1) червяка и корягу за двух мух; 2) двух червей за одну корягу; 3) муху за червяка. Прык-Скок решил на этом обогатиться. У него было только две мухи, но, через несколько обменов, их стало уже четыре. Какое минимальное количество обменов ему потребовалось? (А) 6 (Б) 8 (В) 9 (Г) 10
Галиулина В. Н.
Задача №9
На одной улице посёлка “Большие коты” стоит 40 домов. В 16 из них живёт по одному большому коту, в половине от оставшихся – по два, а в остальных больших котов нет. Сколько всего больших котов живёт на этой улице? (А) 16 (Б) 32 (В) 40 (Г) 48
Тодоров Е. И.
Задача №10
На стол выложены в алфавитном порядке карточки, на которых написаны буквы А, Б, В, Г и Д. На другой стороны каждой карточки написано целое число так, что сумма чисел на любых трёх подряд идущих карточках равна 16. Известно, что на другой стороне карточки в буквой А написано число 3, а на другой карточке с буквой Б написано число 8. Какое число написано с другой стороны карточки с буквой Д? (А) 3 (Б) 8 (В) 5 (Г) 7
Тодоров Е. И.
| Задача № | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Ответ | Б | В | Б | Б | В | Г | Б | Г | В | Б |
I тур: 15 сентября - 27 сентября 2026
II тур: 25 октября 2026
Олимпиада по математике
Двадцать первая международная
Участвуйте в очередной математической олимпиаде от Систематики! Олимпиада проходит в два тура, по итогам которых победители получают ценные призы грамоты и дипломы.
Регистрация участника
Бесплатно


