Задания Двенадцатой Олимпиады по математике Зима 2023 1 тур 2 класс

Задача №1.
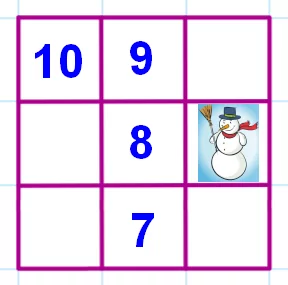
Какое число должно стоять вместо снеговика, если сумма чисел по столбцам, по строкам и по диагоналям одинаковая?

(А) 6
(Б) 9
(В) 12
(Г) 13
(Д) 17

Задача №2.
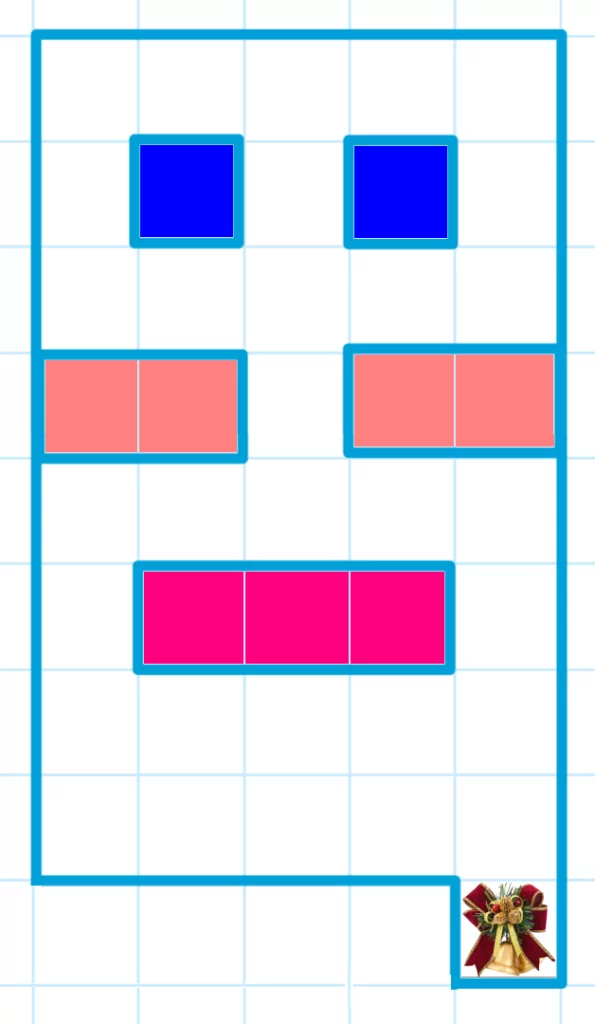
Снеговики нашли кусок льдинки, вырезали буквы и составили из них слово. Какое слово у них могло получиться, если лишних кусков льда не осталось? (Пустые отверстия закрашены другим цветом. Рождественские колокольчики — это часть буквы.)

(А) фон
(Б) зонт
(В) гном
(Г) енот
(Д) снег

Задача №3.
На крыльцо Деда Мороза падали пятилепестковые и шестилепестковые снежинки. Снеговик насчитал всего не более 40 лепестков. Сколько снежинок могло упасть на крыльцо, если шеститилепестковых на 1 больше, чем пятилепестковых?

(А) 6
(Б) 7
(В) 8
(Г) 9
(Д) 10

Задача №4.
Елочку сложили пополам (красная линия) и ещё раз пополам (зелёная линия).Затем сделали три прокола (рис.2). Где будут расположены эти отверстия?

Задача №5
Отражения. Между двумя зеркалами, расположенными как показано на рисунке, поместили знаки римского числа 19 — XIX. Что могло получиться? (Отражение зеркала в другом зеркале не видно).

(А) XIXIXIX
(Б) XIXIXIXIXIX
(В) XXIXXIXXIXX
(Г) XIXXIXXIX
(Д)  XXIIXXIXXIIXX

Задача №6.
Снеговик выложил льдинки-точки, как показано на рисунке.  Если соединить льдинки-точки, то сколько квадратов можно получить с вершинами в этих льдинках-точках?

(А) 6
(Б) 5
(В) 4
(Г) 3
(Д) 2

Задача №7.
Пока ждали Деда Мороза, олени составили вот такой не числовой ребус. Как вы думаете, что должно стоять вместо знака вопроса?

(А) И
(Б) X
(В) Z
(Г) N
(Д) S

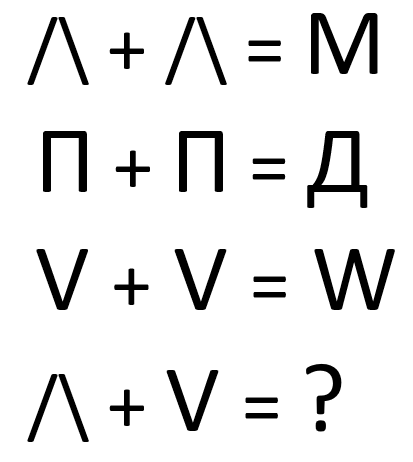
Задача №8.
Снеговик предложил лесным зверям измерить свой рост. Установили, что 1 шаг ежика равен 1 сантиметру. Когда очередь дошла до ужа, его решили измерить в шагах. У  медведя — 4 шага. Какой длины уж, если 1 шаг зайца равен 2 шагам ежа, а 1 шаг медведя равен 4 шагам зайца?

(А) 310 мм
(Б) 28 см
(В) 420 мм
(Г) 32 см
(Д) 24 см

Задача №9.
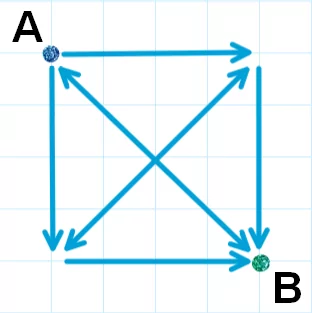
Снеговик развозил новогодние подарки по кварталу, как показано на рисунке (стрелками указаны направления движения Снеговика). Сколько различных маршрутов с начальной точкой А и финальной точкой В мог пройти Снеговик, если по каждой линии можно пройти не более одного раза?

(А) 5
(Б) 6
(В) 7
(Г) 8
(Д) 9

Задача №10.
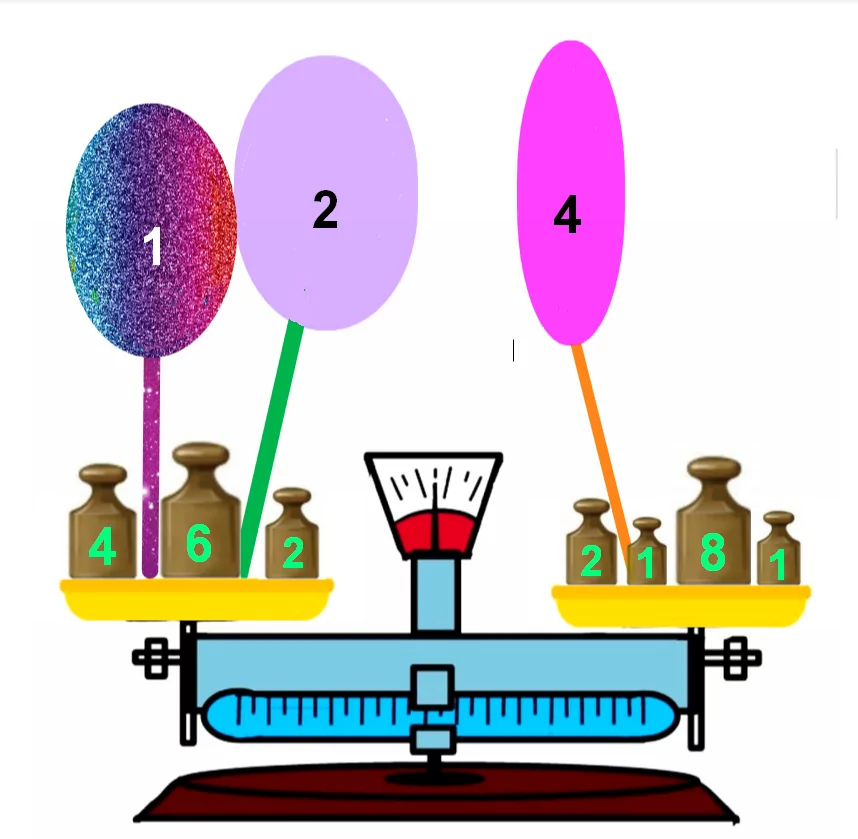
Снеговик изучал взвешивания. На чашечные весы, изображенные на рисунке, он поставил гири и привязал шарики к чашам весов. На каждой гире указан вес самой гири, а на шарике указан вес, который этот шарик может поднять. Какая чаша весов легче и на сколько килограмм?

(А) правая на 1 кг тяжелее
(Б) левая на  1 кг тяжелее
(В) весы находятся в равновесии
(Г) левая на  3 кг тяжелее
(Д) правая на 3 кг тяжелее