Куда поехать с ребёнком летом?
6 лучших идей для семейного путешествия!
Задания 2-го тура XI олимпиады по математике для 9 класса
2-ой тур XI олимпиады по математике прошел 23 октября 2022 года.
Задача №1
В прямоугольном треугольнике АВС с прямым углом С, гипотенуза АВ = 20 см. Может ли его площадь быть равной 110 см2?
Задача №2
Маша нарисовала квадрат по клеточкам. Катя вырезала из него другой квадрат по клеточкам. При этом от Машиного квадрата не вырезанными остались 37 клеточек. Чему равна сторона Машиного квадрата? Найти все варианты и доказать, что других вариантов нет!
Задача №3
Сколькими способами можно расставить в ряд числа 1, 2, 3, 4, 5, 6 так, что второе число отличается от первого, третье число — от второго, четвёртое - от третьего, пятое - от четвертого, шестое число — от пятого на целое число процентов?
Задача №4
Дана трапеция ABCD, в которой AB=BC=CD и P — основание перпендикуляра, опущенного из точки C на основание AD. Докажите, что если из точки P опустить перпендикуляр на диагональ AC, то он проходит через середину диагонали BD.
Задача №5
Известно, что натуральные числа a, b, c удовлетворяют соотношению a+b=ab-bc, а c+1 — квадрат простого числа. Докажите, что хотя бы одно из чисел a+b или ab является квадратом натурального числа.
Задача №6
В вершинах шестиугольника написали натуральные числа (не обязательно различные), а на каждой стороне — НОК чисел, написанных на ее концах. Могло ли оказаться, что числа на сторонах — это шесть последовательных чисел? (Если да, то приведите пример чисел, написанных в вершинах, если нет, то объясните почему такого быть не может)
Задача №7
Имеется клетчатая доска 5×6, первоначально пустая. За один ход можно поставить на любую из пустых клеток одну фишку: белую, если в “кресте” с этой клеткой находится чётное число фишек, чёрную – если нечётное. Какое наибольшее число белых фишек можно поставить на доску? (“Крест” - это клетки, которые находятся с данной клеткой в одном столбце или одной строке)
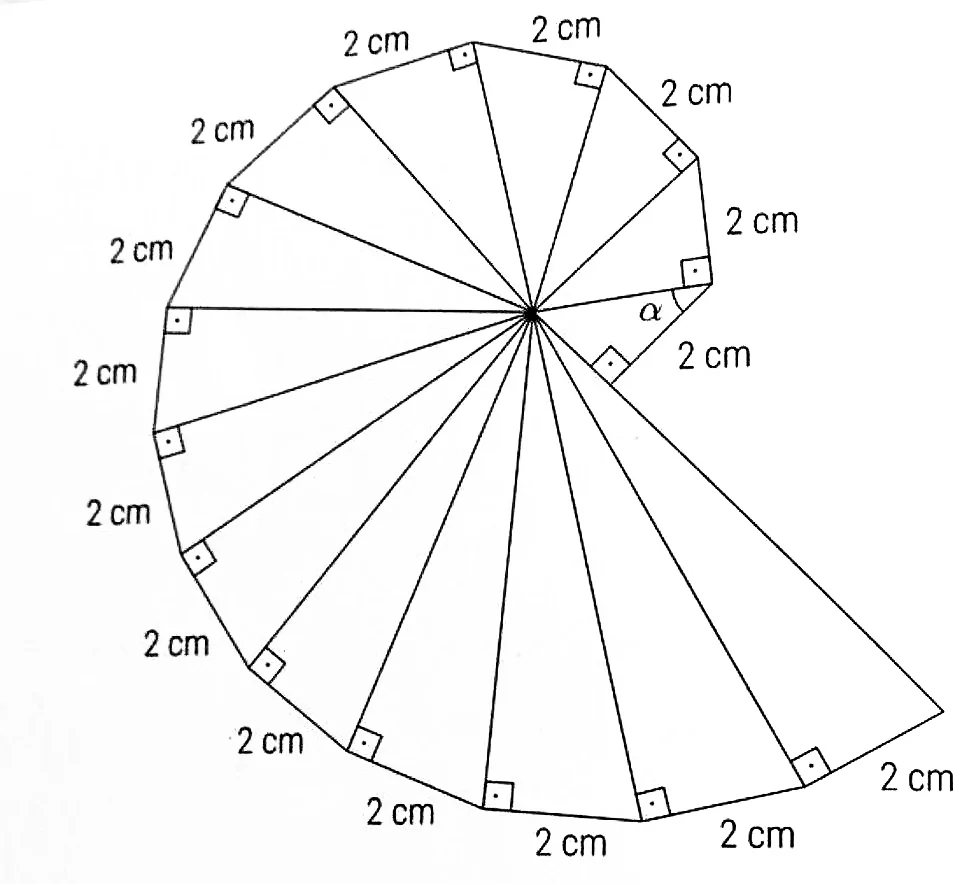
Задача №8
Найти угол α , если самая большая сторона равна 8 см.
Решения и ответы

Пробная олимпиада
Пройдите пробную олимпиаду по математике для 1–9 классов.
1-й тур: 15 – 29 сентября
2-й тур: 20 июля
Олимпиада по математике
Девятнадцатая международная олимпиада по математике
Участвуйте в очередной математической олимпиаде от Систематики! Олимпиада проходит в два тура, по итогам которых победители получают ценные призы грамоты и дипломы.
Зарегистрироваться
Бесплатно