Как успешно написать олимпиаду
Курс прошли 3 000 учеников! Присоединяйтесь к подготовке
Задания 2-го тура XIV олимпиады по математике для 9 класса

Только сегодня до 23:59
2-ой тур XIV олимпиады по математике прошел 29 октября 2023 года.
Задача №1
Яша и Зюзя изобрели свои температурные шкалы. Яша принял за 0 температуру, при которой у него замерзает левая пятка, а 1 градус по его шкале - это то, насколько нагревается камешек, если Яша держит его в руке ровно минуту. А Зюзя принял за 0 температуру, при которой он начинает шмыгать носом и чихать, а за 1 градус принимает то, как меняется температура железного шарика, если Зюзя дышит на него ровно минуту. Каждый из изобретателей сделал термометр для своей шкалы и пошли мерить всё на свете. Оказалось, что если нагреть что-то на 1 градус по шкале Яши, то оно нагреется на 2 градуса по шкале Зюзи; а ещё оказалось, что 0 по шкале Зюзи равен 6 по шкале Яши. Какая температура будет выражаться одинаковым числом градусов по обеим шкалам?
Задача №2
Напишите следующие два числа в последовательности: 1,6,21,56… И объясните закономерность.
Задача №3
Известно, что корнями уравнения x^2 +bx + c = 0 являются числа 2^n и 6^k при некоторых натуральных числах n и k. Вовочка говорит, что если подставить в это уравнение вместо x число 27, то получится 2023. Прав ли он?
Задача №4
Дан треугольник ABC. Его вписанная окружность касается сторон AB и BC в точках K и L соответственно. Вневписанная окружность треугольника ABC, касающаяся стороны AC, касается продолжений сторон BA и BC за точки A и C в точках M и N соответственно. Биссектриса угла BAC пересекает прямую KL в точке X. Биссектриса угла ACN пересекает прямую MN в точке Y. Докажите, что прямая XY параллельна биссектрисе угла ABC.
Задача №5
Известно, что x+y=15. Каким будет минимальное значение выражения ?
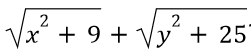
Задача №6
На плоскости дано конечное число окружностей, любые две из которых пересекаются в двух точках. Они разбили плоскость на области. Можно ли расставить в областях положительные числа так, чтобы для каждой окружности суммы чисел внутри и снаружи были бы равны?
Задача №7
Назовём число n суммоквадратовым, если существует табличка 2n, в первой строке которой записаны числа от 1 до n(каждое по одному разу в строке) в прямой последовательности, а во второй - в какой-то другой, а сумма в каждом столбике является квадратом некоторого натурального числа. Например, числа 3 и 5 являются суммоквадратовыми, потому что существуют таблицы 1 2 3 3 2 1 и 1 2 3 4 5 3 2 1 5 4, в которых сумма в каждом столбике будет точным квадратом. Докажите, что суммоквадратовых чисел бесконечно много.
Задача №8
Четверо рассеянных гномов нашли три двенадцатикилограммовых золотых самородка и хотят разделить их на троих так, чтобы каждый получил одинаковый суммарный вес золота. Для этого они разбивают самородки на куски и собирают свою долю из них. Известно, что если кому-то из рассеянных гномов попадётся кусок, весящий 3 килограмма или меньше, он обязательно потеряет его на обратном пути. Докажите, что на обратном пути будет потерян хотя бы один кусок золота.

Пробная олимпиада
Пройдите пробную олимпиаду по математике для 1–9 классов.
1-й тур: 15 – 29 сентября
2-й тур: 20 июля
Олимпиада по математике
Девятнадцатая международная олимпиада по математике
Участвуйте в очередной математической олимпиаде от Систематики! Олимпиада проходит в два тура, по итогам которых победители получают ценные призы грамоты и дипломы.
Зарегистрироваться
Бесплатно


