Календарь олимпиад
Задания 2-го тура XIII олимпиады по математике для 9 класса

Ваш личный проводник в мир олимпиад по математике.
Регистрация. Советы. Подготовка.
2-ой тур XIII олимпиады по математике прошел 9 июля 2023 года.
Задача №1
Два натуральных числа a и b назовём дружественными к друг другу, если для чисел x = НОД(a, b), y = a/x и z=b/x, существует невырожденный треугольник с длинами сторон x, y и z. Опишите все пары натуральных дружественных чисел таких, что треугольники со сторонами x, y и z, будут равнобедренными.
Задача №2
Есть карточки с числами 123, 124, 134, 234 (с каждым числом - сколько угодно карточек). Можно ли разложить их по кругу так, чтобы у каждой пары чисел, стоящих рядом, была одинаковая цифра, и каждая пара чисел с одинаковой цифрой встречалось рядом ровно один раз?
Задача №3
В выпуклом четырехугольнике ABCD ∠A = ∠D = ½∠B, ∠ABD = 87◦. Из точек B и C опустили высоты BM и CN на сторону AD. В результате оказалось, что удвоенная сумма AM и DN равна AB + CD. Найдите ∠CAD
Задача №4
Вычислите сумму x+y+z, если известно что:
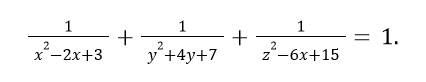
Задача №5
Дракон пересчитал свои сокровища и решил построить на них новую башню из 10 этажей. В башне планируются этажи двух типов: с окнами и без. Дракон любит блеск солнечных лучей на своём золоте, поэтому хочет, чтобы на самом верхнем этаже обязательно было окно, и чтобы никакие два соседних этажа не могли одновременно быть без окон. Сколько различных башен подойдёт под требования дракона? (Различными будем считать башни, отличающиеся наличием или отсутствием окон хотя бы на одном этаже.)
Задача №6

Задача №7
Пять футболистов выстроились в ряд. У каждого на футболке написан номер от 1-го до 5-ти (все номера разные). Каждый футболист посчитал количество людей с номером, меньшим чем у него и стоящих по правую руку от него. Сумму посчитаных чисел назвали. После, они передвинулись циклически (первый перешел в конец шеренги), повторили предшествующие действия, назвали новое число и передвинулись снова. Повторили все несколько раз. В результате, были названы числа 6, 4, 8, 4, 4. В каком порядке стояли футболисты изначально?
Задача №8
Царевна-лягушка с одинаковой вероятностью называет любое целое число от -5 до 5, а Императрица-жаба - от -7 до 7. Вы можете выбрать любое земноводное, после чего они одновременно выквакивают загаданные числа. Если у выбранного Вами земноводного число больше - Вы побеждаете. Если меньше, то проигрываете. Если равны, то Вы можете заново выбрать земноводное и попросить их загадать числа ещё раз. Кого Вам стоит выбрать, чтобы увеличить вероятность выигрыша?
Скачать задания в формате PDF
Решения и ответы

Пробная олимпиада
Пройдите пробную олимпиаду по математике для 1–9 классов.
1-й тур: 13 января — 26 января
2-й тур: 27 октября
Олимпиада по математике
СЕМНАДЦАТАЯ МЕЖДУНАРОДНАЯ ОЛИМПИАДА СИСТЕМАТИКИ
Участвуйте в очередной математической олимпиаде от Систематики! Олимпиада проходит в два тура, по итогам которых победители получают ценные призы грамоты и дипломы.
Зарегистрироваться
Бесплатно



