Задания Тринадцатой Олимпиады по математике Весна 2023 1 тур 9 класс

1 тур олимпиады по математике прошёл с 15 мая по 7 июня 2023 года

Задача №1
Рассмотрим 2 рекорда, установленных в 2019 и 2020 годах:
1) Самец малого веретенника преодолел около 12200 километров над Тихим океаном во время миграции с Аляски в Новую Зеландию за 11 дней.
2) За 24 часа владелец Tesla Model 3 проехал путь длиной 2781 км. Для того, чтобы избежать усталости во время пути, в салоне было еще два водителя- когда уставал один — за руль садился второй, потом — третий.
Исходя из того, что для опытных водителей не рекомендуется при длительных поездках проводить за рулём больше 12 часов в сутки, найдите за какое время одиночный водитель преодолеет такое же расстояние, как и птица (остальные условия движения в среднем такие же, как и при установке рекорда)? Результат округлить с точность до 1/10 часа
(А) 8 суток 18,6 часа
(Б) 8 суток 9,3 часа
(В) 9 суток 6,6 часа
(Г) 4 суток 9,3 часа
(Д) 7 суток 11,3 часа

Задача №2
Машенька вырезала из квадратного листочка в клеточку квадрат меньшего размера, ровно по границам клеточек. Какого максимального размера мог быть первоначальный квадрат если остался кусочек площадью в 1349 клеточек. Введите число — сторону первоначального квадрата.

Задача №3
Найдите площадь поверхности указанного тела, состоящего из единичных кубиков.
Нижняя часть симметрична верхней.

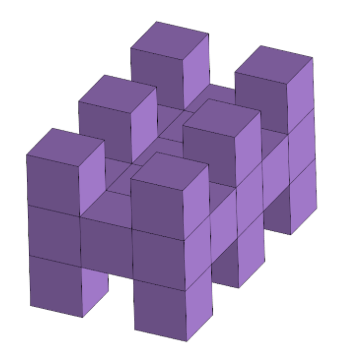
Задача №4
Площадь фигуры, образованной пересечением линий:
8х + 2|y| = 3
3x — 6|y| = 1
равна…

(А) 0
(Б) 1/1296
(В) 1/288
(Г) 1/796
(Д) 3/4096

Задача №5
У вас есть набор палочек, лежащих в виде сетки. Вы забираете палочки по одной начиная с самого верха. Чему будет равно значение полученного выражения?
Пожалуйста, не забывайте про порядок действий. В ответ введите число.

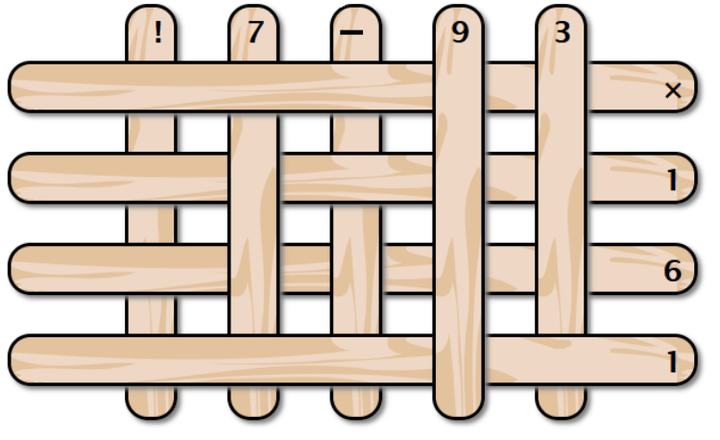
Задача №6
Расставьте в выражении цифры от 1 до 9 так чтобы получилось верное равенство.
У равенства есть несколько ответов. Чему равна разница самого большого и самого маленького из центральных чисел, удовлетворяющих условию задачи?

Задача №7
Сколько решений имеет уравнение (решения считаются различными, если хотя у них отличается хотя бы одно из чисел в паре (x, y))?

(А) 2
(Б) 6
(В) 8
(Г) 14

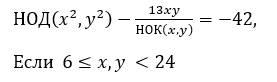
Задача №8
Дано число. Сколько у этого числа делителей?

Задача №9
В клетчатой фигуре вырезали дырку (см. картинку). Сколько в этой фигуре прямоугольников?

(А) 15
(Б) 64
(В) 80
(Г) 100
(Д) 128

Задача №10
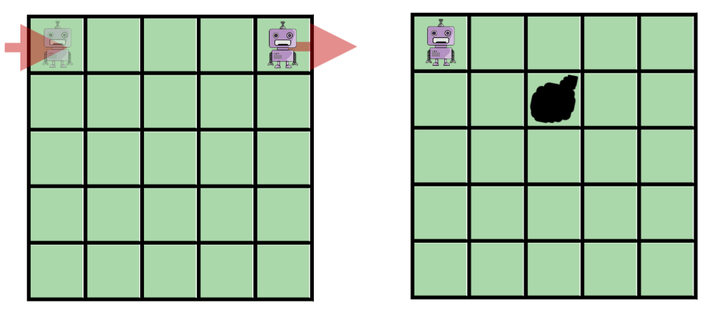
Слепой робот-уборщик может передвигаться по полю только вниз и вправо. Как только он выходит за пределы поля он мгновенно материализуется на другой стороне поля (как показано на рисунке, за один шаг робот переместится из крайней правой клетки в крайнюю левую). В середине поля 19×19 лежит куча мусора. Поскольку робот не может ее видеть, он действует так: сначала делает 24 шага вправо, потом 22 шага вниз и повторяет эти действия до тех пор, пока куча не будет найдена. Через сколько ходов поле станет чистым? Робот стартует из левой верхней клетки. Рисунок дан для примера на поле меньшего размера.

(А) Никогда
(Б) 18
(В) 68
(Г) 151
(Д) 227