Задания Четырнадцатой Олимпиады по математике Осень 2023 1 тур 9 класс

Задача №1.
У вас есть набор палочек лежащих в виде сетки. Вы забираете палочки по одной начиная с самого верха. Чему будет равно значение полученное выражение? Пожалуйста, не забывайте про порядок действий. В ответ введите число.

Задача №2.
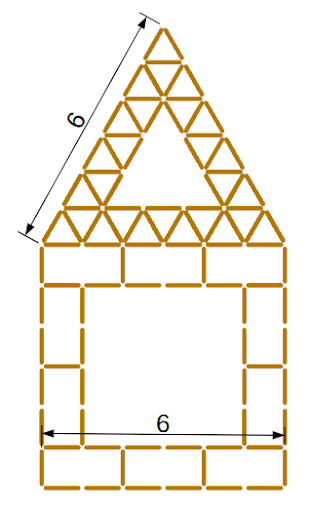
Лёша складывает из спичек фигурку домика по образцу (см. Рис). К треугольнику он пристроил часть домика с таким же размером.
Сколько спичек придётся потратить на эту фигуру со стороной равной 15? Введите число в ответе.

Задача №3.
Сколько чисел, делящихся на 11, можно составить из цифр 0, 1, 2, 3,…,8 (каждую цифру использовать ровно по одному разу)?

(А) 18432
(Б) 23040
(В) 11520
(Г) 9216
(Д) 28800

Задача №4.
У Гринча в мешке лежат 104 цифры «1». Он составил из них несколько (четное количество) чисел. Потом разбил их на пары и перемножил. Какой наибольшее суммарное количество цифр «5» он мог получить?

(А) 14
(Б) 54
(В) 78
(Г) 95
(Д) 96

Задача №5
Несколько игроков участвовали турнир по шахматам (каждый сыграл с каждым по разу). Оказалось, что в каждой группе из n (n ≥ 2) игроков нашелся человек, выигравший всех из этой группы. При каком минимальном количестве игроков такое могло произойти?

(А) 2^n-1
(Б) 2^n+1
(В) 2^(n+1)-1
(Г) 2^(n+1)
(Д) 2^(n+1)+1

Задача №6.
Числа от 1 до 100 выписали в ряд в некотором порядке. Натуральное число n ⩽ 100 называется интересным, если сумма первых n чисел в ряду равна n2. Какое наибольшее количество интересных чисел может быть?

(А) 11
(Б) 24
(В) 25
(Г) 50
(Д) 51

Задача №7.
В пятиугольнике ABCDE AB=3, AC=5, AD=13, AE=85, BC=4, CD=12, DE=84.
Чему равна площадь пятиугольника?

(А) 1164
(Б) 498
(В) 582
(Г) не хватает данных

Задача №8.
Вася выписывает на доску все наборы, составленные из чисел 12, 21, 17, 71, 19 и 91, причём в каждом наборе все числа различны. Сколько наборов, в которых будет хотя бы одно простое число, выпишет Вася?

(А) 24
(Б) 64
(Г) 48
(Д) 56

Задача №9.
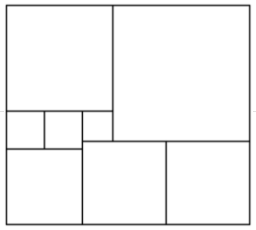
Прямоугольник разбили на 8 квадратов (см. рисунок). Сторона самого маленького квадрата (в центре) равна 6. Чему равна площадь прямоугольника?

(А) 2088
(Б) 2754
(Г) 1827
(Д) 2160

Задача №10.
Из цифр 1, 2, 3, 4, 5 и 6 составили всевозможные двузначные числа с неповторяющимися цифрами. Найдите сумму всех этих чисел.

(А) 231
(Б) 720
(Г) 1155
(Д) 1296