Задания 2-го тура XIV олимпиады по математике для 9 класса
2-ой тур XIV олимпиады по математике прошел 29 октября 2023 года.
Задачи олимпиады
Задача №1
Яша и Зюзя изобрели свои температурные шкалы. Яша принял за 0 температуру, при которой у него замерзает левая пятка, а 1 градус по его шкале - это то, насколько нагревается камешек, если Яша держит его в руке ровно минуту. А Зюзя принял за 0 температуру, при которой он начинает шмыгать носом и чихать, а за 1 градус принимает то, как меняется температура железного шарика, если Зюзя дышит на него ровно минуту. Каждый из изобретателей сделал термометр для своей шкалы и пошли мерить всё на свете. Оказалось, что если нагреть что-то на 1 градус по шкале Яши, то оно нагреется на 2 градуса по шкале Зюзи; а ещё оказалось, что 0 по шкале Зюзи равен 6 по шкале Яши. Какая температура будет выражаться одинаковым числом градусов по обеим шкалам?
Тодоров Е. И.
Задача №2
Напишите следующие два числа в последовательности: 1,6,21,56… И объясните закономерность.
Иванюк Д. В.
Задача №3
Известно, что корнями уравнения x^2 +bx + c = 0 являются числа 2^n и 6^k при некоторых натуральных числах n и k. Вовочка говорит, что если подставить в это уравнение вместо x число 27, то получится 2023. Прав ли он?
Тодоров Е. И.
Задача №4
Дан треугольник ABC. Его вписанная окружность касается сторон AB и BC в точках K и L соответственно. Вневписанная окружность треугольника ABC, касающаяся стороны AC, касается продолжений сторон BA и BC за точки A и C в точках M и N соответственно. Биссектриса угла BAC пересекает прямую KL в точке X. Биссектриса угла ACN пересекает прямую MN в точке Y. Докажите, что прямая XY параллельна биссектрисе угла ABC.
Нилов Ф. К.
Задача №5
Известно, что x+y=15. Каким будет минимальное значение выражения ?
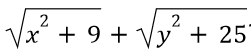
Тодоров Е. И.
Задача №6
На плоскости дано конечное число окружностей, любые две из которых пересекаются в двух точках. Они разбили плоскость на области. Можно ли расставить в областях положительные числа так, чтобы для каждой окружности суммы чисел внутри и снаружи были бы равны?
Нилов Ф. К.
Задача №7
Назовём число n суммоквадратовым, если существует табличка 2n, в первой строке которой записаны числа от 1 до n(каждое по одному разу в строке) в прямой последовательности, а во второй - в какой-то другой, а сумма в каждом столбике является квадратом некоторого натурального числа. Например, числа 3 и 5 являются суммоквадратовыми, потому что существуют таблицы 1 2 3 3 2 1 и 1 2 3 4 5 3 2 1 5 4, в которых сумма в каждом столбике будет точным квадратом. Докажите, что суммоквадратовых чисел бесконечно много.
Тодоров Е. И.
Задача №8
Четверо рассеянных гномов нашли три двенадцатикилограммовых золотых самородка и хотят разделить их на троих так, чтобы каждый получил одинаковый суммарный вес золота. Для этого они разбивают самородки на куски и собирают свою долю из них. Известно, что если кому-то из рассеянных гномов попадётся кусок, весящий 3 килограмма или меньше, он обязательно потеряет его на обратном пути. Докажите, что на обратном пути будет потерян хотя бы один кусок золота.
Тодоров Е. И.
I тур: 15 сентября - 27 сентября 2026
II тур: 25 октября 2026
Олимпиада по математике
Двадцать первая международная
Участвуйте в очередной математической олимпиаде от Систематики! Олимпиада проходит в два тура, по итогам которых победители получают ценные призы грамоты и дипломы.
Регистрация участника
Бесплатно


