II олимпиада по математике прошла 14 января 2018 года.
Задачи олимпиады
Задание №1
На картинке 6 снежинок. Если выбрать 3 из них и поменять местами по циклу по часовой стрелке (первая на место второй, вторая на место третьей, третья на место первой) или аналогично против часовой стрелки, то снежинки выстроятся в порядке убывания. Обведите снежинки, которые нужно переставить и нарисуйте стрелками, в какую сторону их надо переставлять.

Задание №2
Разделите фигуру вдоль линий сетки на три равные по форме и размеру части.

Задание №3
Антон, Боря, Вася, Гога, Даня построились на физкультуру. Антон в очках. Боря носит шорты в горошек. Вася кудрявый. Гога не с краю. Даня не самый высокий. Антон выше Гоги. У Васи и Бори разные причёски. Подпиши имя каждого мальчика.

Задание №4
Аня и Петя решают один и тот же набор головоломок. Аня на одну головоломку тратит 2 минуты, а Петя — 3 минуты. Известно, что Петя потратил на всю работу на 10 минут больше, чем Аня. Сколько головоломок в наборе? Напишите ответ и объяснение.
Задание №5
Каждая мартышка съела по 1 апельсину, 5 бананов и 3 яблока. А каждая макака съела по 2 банана, 4 яблока и 6 апельсинов. Сколько было съедено яблок, если апельсинов и бананов все вместе съели 100 штук? Напишите ответ и объяснение.
Задание №6
Расставьте числа от 1 до 7 по одному разу в кружки так, чтобы суммы вдоль всех линий были равны (круг — тоже линия).
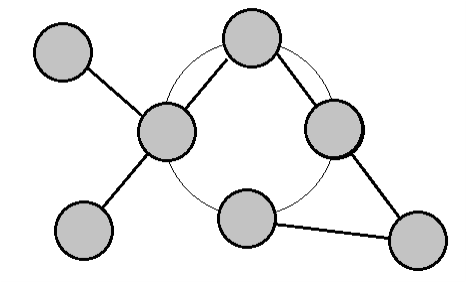
Задание №7
Набор домино содержит 28 различных доминошек, содержащих пары, на каждой половинке — от 0 до 6 точек. Ника выкинула из набора все костяшки, где хотя бы на одной из половинок было больше 4 точек. Остальные костяшки она выложила на стол как на картинке. Нарисуйте границы доминошек. Помните: все доминошки уникальные и не могут повторяться.
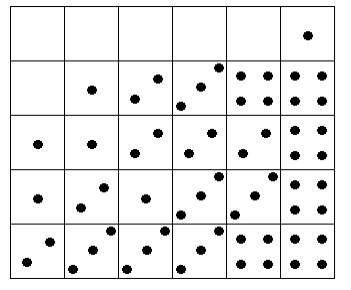
Задание №8
В классе три ряда по 4 парты. На первом ряду и на всех первых партах сидят в сумме 9 человек. На втором ряду в сумме со вторыми партами сидят 8 человек. На третьему ряду в сумме со всеми третьими партами сидят 9 человек. На четвертых партах всего сидят 2 человека. Сколько человек в классе? Напишите ответ, объяснение и нарисуйте на схеме как могут сидеть ребята.
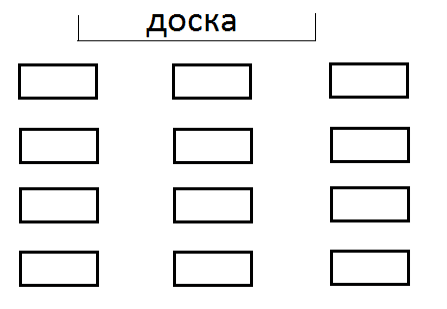
Ответы на задачи №1-8 в формате разборов
I тур: 15 сентября - 27 сентября 2026
II тур: 25 октября 2026
Олимпиада по математике
Двадцать первая международная
Участвуйте в очередной математической олимпиаде от Систематики! Олимпиада проходит в два тура, по итогам которых победители получают ценные призы грамоты и дипломы.
Регистрация участника
Бесплатно



