Разбор заданий конкурса Кенгуру по математике. 18 марта 2021. 8 класс

Решения:

Задача 1
Правильный ответ: В

Диагональ разбила четырехугольник на два треугольника, у которых она является общей стороной. Для сторон треугольника должно выполняться неравенство: сумма двух, даже самых маленьких сторон, должна быть больше третьей. Подбираем возможные варианты. Из предложенных чисел можно составить только два треугольника: один – со сторонами 1, 2, 2,8, а другой – 2,8; 5; 7,5. Общей стороной является сторона длиной 2,8 – значит, это и есть искомая диагональ.

Задача 2
Правильный ответ: А

Ось симметрии есть только у одного из этих знаков – это Стрелец. Она совпадает с центральной линией «стрелки». Остальные приведенные знаки симметрией не обладают

Задача 3
Правильный ответ: Д

Фиксируем вертикальный диаметр, и серый цвет из фигур справа от диаметра переносим в равные им фигуры слева от диаметра. Закрасится полкруга, 50%

Задача 4
Правильный ответ: Б

Строим их, начиная с самого маленького: 1234, 2345, 3456, 4567, 5678, 6789. Всего 6.

Задача 5
Правильный ответ: А

Складывая паззл, получим пример 2–102. Ответ: -100

Задача 6
Правильный ответ: Б

Складываем столбиком, опираясь на решенный верно пример для двухзначных чисел, или используя сумму разрядных слагаемых. Ясно, что В+D=7 или 17, а А+С=13 или 12. Для суммы четырехзначных чисел получится: 1000∙(А+С)+100∙(В+D)+10∙(С+А)+1∙(В+D) = 1000∙13+100∙7+10∙13+1∙7=13837. Для второго варианта ответ тот же.

Задача 7
Правильный ответ: Б

По условию каждое колесико поворачивается на половину оборота. На колесике цифры: 0 и 5, 1 и 6, 2 и 7, 3 и 8, 4 и 9 — будут находиться диаметрально противоположно. Поэтому для ответа выбираем диаметрально противоположные цифры для 6348. Получим число 1893. Это вариант Б.

Задача 8
Правильный ответ: Д

Достаточно изобразить отрезками рост мальчиков, и ответ будет ясен.
Другой вариант: пусть рост Антона — х, тогда Бори – (х+5), Вани – (х+15), Гриши – (х+25), Димы – (х+30). Значит Дима выше Антона (или Антон ниже Димы, как предложено в ответах) на 30 см.

Решения:

Задача 9
Правильный ответ: Г

Согласно условию, одна сторона шоколадки содержит 6 квадратов (12÷2=6) а другая 11 квадратов (9+2=11). Ясно, что отламывали от шоколадки с разных сторон плитки. Всего в плитке 11∙6=66 квадратов. Съели 12+9=21 квадрат, тогда осталось 66-21=45 квадратов.

Задача 10
Правильный ответ: Д

Пусть вес банки равен х, а вес воды в полной банке у.
Тогда по условию имеем: (х+ 4/5у)–(х+ 1/5у)=740–560.
Отсюда находим у — вес воды в банке (у), он равен 300 г.
Теперь по первому условию получаем: 560–300÷5=500 г – вес пустой банки.

Задача 11
Правильный ответ: В

Согласно условию, сторона большого квадрата будет равна 4 см (т.к. площадь равна 16 кв.см). Находим площадь белого треугольника. Его основание будет равно 2 см, и высота тоже 2. По формуле площадь одного такого треугольника равна 2 кв.см, а площади четырех таких треугольников — 8 кв.см. Тогда площадь черных фигур – это площадь большого квадрата минус площади четырех серых квадратов и четырех белых треугольников. 16–8–4=4 кв.см.

Задача 12
Правильный ответ: В

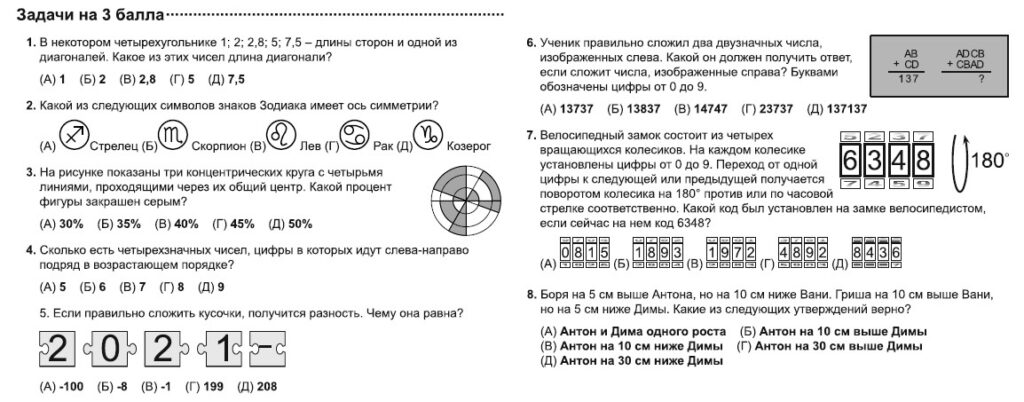
Обозначим сторону самого большого квадрата как у. Тогда сторона нижнего левого квадрата будет иметь длину (у-1), сторона верхнего левого – длину (у-2), а верхнего справа от него – длину (у-3). Используя это выражение, получим, что длина самого большого квадрата может быть записана как (у-4)+h. Но она же у нас была принята за у.
Получаем: (у-4)+h=у. Отсюда находим, что h=4.

Задача 13
Правильный ответ: Б

Пусть х – количество вопросов с правильными ответами, у – с неправильными, z – вопросы без ответов.
Тогда имеем: х+у+z =20, 7х–4у=100. Тогда 7х=100+4у.
Подбираем у, учитывая, что 100+4у кратно 7. Подходит у=3. В этом случае х=(100+4∙3)÷7=16, а z=20-3-16=1.
Отметим, что также подходит у=10, но в этом случае х=20, не соответствует условию (всего 20 вопросов). Значит ответ: 1 вопрос остался без ответа.

Задача 14
Правильный ответ: В

У прямоугольника с площадью Р стороны равны х и 4, значит Р=4х. Стороны треугольника с углом 450 равны между собой и равны 4 см, и этот треугольник является половиной квадрата со стороной 4 и площадью 16 (т.к в этом месте лист согнут в два слоя). Площадь Q в 2 раза меньше площади Р и будет равна 4х÷2=2х. Площадь всего прямоугольника равна 13∙4=52. Тогда получаем: 4х+2х+16=52. Отсюда находим, что х=6.

Задача 15
Правильный ответ: Д

Пусть в корзине лежит 2А яблок, и такое же количество фруктов получила Кристи. Пусть у нее х яблок, тогда груш (2А–х). Лили получила А фруктов, у нее яблок (2А–х), и их количество равно количеству груш у Кристи.

Задача 16
Правильный ответ: В

Данная дробь — а/b. Новая дробь, которую получили увеличением числителя на 40% — 1,4а/хb и она вдвое больше исходной.
Получим: 2а/b=1,4а/хb.
Отсюда 2ахb=1,4аb. Получаем, что х=0,7.
Это означает, что х=70% от b. Значит, знаменатель b уменьшили на 30%

Решения:

Задача 17
Правильный ответ: Г

Вершина пирамиды – D. Второй ряд содержит ядра с буквами А,В,С. Третий ряд – ядра с буквами В,Е,D,С,Е,А. Четвертый ряд – D,Е,С,А,Е,В,С,В,А и невидимое ядро с неизвестной буквой. Так как каждая буква должна присутствовать на 4 ядрах, то проверяем и находим, что не достает метки D.

Задача 18
Правильный ответ: Б

Число 1ABCDE умножаем на 3 столбиком. При умножении Е на 3 на конце 1, значит, Е=7, запоминаем 2.
D умножаем на 3 и прибавляем 2, на конце 7, значит, D=5, запоминаем 1.
С умножаем на 3 и прибавляем 1, на конце 5, значит, С=8, запоминаем 1.
В умножаем на 3 и прибавляем 2, на конце 8, значит, В=2
А умножаем на 3, на конце стоит 2, значит, А=4, запоминаем 1.
1 умножаем на 3 прибавляем 1, получим 4 – это А.
Все сошлось. Число 142857. Сумма его цифр равна 27.

Задача 19
Правильный ответ: Б

Задача на принцип Дирихле. Сумму всех фишек примем за х. Тогда наименьшее количество фишек каждого цвета будет равняться:
х–26 = зеленые
х–24 = красные
х–21 = синие
х–16 = желтые.
Складывая, получим уравнение: 4х–87=х, откуда получаем, что х=29 – наименьшее количество фишек.

Задача 20
Правильный ответ: Г

10 шестиугольников на видимой части мяча и столько же на невидимой. Всего 20.

Задача 21
Правильный ответ: Г

Возможны два случая отбора для образования пар: один случай — 20 рыцарей и 2000 лжецов, второй случай – 21 рыцарь и 1999 лжецов.
Рассмотрим первый вариант: 20 рыцарей и 2000 лжецов. Возможно три варианта пар: (лжец, лжец) – пусть х пар, (лжец, рыцарь) = (2000–2х÷у) – у пар по количеству рыцарей, которые вошли в эту пару; (рыцарь, рыцарь) – (20–у) ÷2 пар.
Первая пара назовет рыцарями 2х человек, лжецами никого; вторая пара назовет лжецами (2000–2х+у) человек, рыцарями никого; третья пара назовет рыцарями (20–у) человек, лжецами никого.
Всего 1010 пар, 20 человек названы лжецами и 2000 человек названы рыцарями, составляем уравнения:
х+у+(20–у)÷2 = 1010
2х+20–у=2000
2000–2х+у=20.
Решая их, получим х=995 – столько было пар лжецов.
Второй случай не подойдет, так как х получится не целым числом, что противоречит условию.

Задача 22
Правильный ответ: В

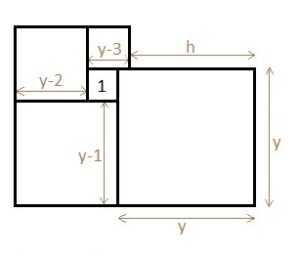
Соединим точку К со всеми вершинами четырехугольника, тогда образуется 8 треугольников. Будем сравнивать их площади, применяя свойство площадей треугольников: площади треугольников, у которых высота одинаковая, относятся как основания. Площадь треугольника МКВ (см. рисунок в первом комментарии) примем за х, а площадь треугольника ВКР за у. На рисунке указаны площади других треугольников, выраженные через х и у. Нужно найти (х+у). Используя четырехугольник с площадью 18, получим уравнение: 6+2у+2х=18, откуда х+у=6.

Задача 23
Правильный ответ: Б

Считаем окрашенные грани. Они будут у 8 кубиков в вершинах и у 3 кубиков на одном ребре, кроме тех, которые образуют вершины. Итого на всех ребрах получится 3∙12=36 кубиков. Внутри каждой грани останется 9 покрашенных кубиков, которые не в вершинах и не на сторонах. Тогда во всех гранях 9∙6=54 кубика. Складываем и получаем общее количество интересующих нас кубиков: 8+36+54=98.

Задача 24
Правильный ответ: Г

Точка пересечения вершин всех треугольников является общей вершиной 5 равных углов, сумма которых 360 градусов. Тогда один угол равен 360÷5=72 градуса. Другой острый угол треугольников будет равен 90-72=18 градусов. Чтобы построить звезду нужно 360÷18=20 треугольников.