Задания 1-го тура XV олимпиады по математике для 2 класса

У доктора Фасилье есть пара заколдованных кубиков, один – черного, другой – красного цвета. При броске одновременно красного и черного кубиков, сумма выпавших чисел на них всегда равна 7. Принц Навин подсчитал, что сумма всех выпавших чисел на красном кубике за три таких броска равна 9. Чему равна сумма чисел на черном кубике за эти же броски?

48 детей водили хоровод вокруг новогодней елки. При этом, каждый мальчик держал за руки двух девочек, а каждая девочка – девочку и мальчика. Сколько мальчиков было на празднике?

На картинке ниже цифрами обозначены люди: 1 — Егор; 2 — Лиза; 3 — Маша; 4 — Саша; 5 — Олег; 6 — Герман; 7 — Полина; 8 — Карина; 9 — Тимофей. Линии между цифрами показывают кто с кем дружит. Определите у кого больше всего друзей.

Вероника собирала бусы в подарок и располагала бусины в следующем порядке: синяя круглая, красная розочка, 2 зелёных лепесточка, синяя круглая, красная розочка, и так далее. Сколько синих бусин Веронике потребовалось для бус, если последняя бусина была синяя круглая и на бусы ушло 9 красных розочек?

Одинаковыми фигурами зашифрованы одинаковые цифры. Разными – разные. Какая цифра зашифрована оранжевым треугольником?

Какое наименьшее количество веточек нужно отрезать, чтобы все красные ёлочные игрушки упали, а все шары остались?

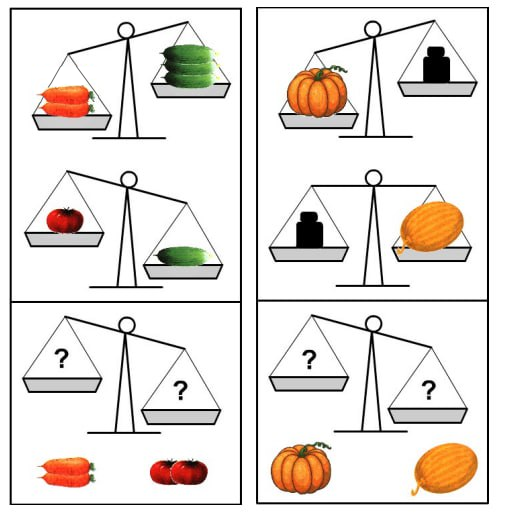
Что покажут весы?

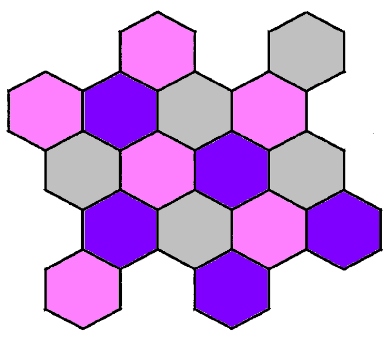
На сколько равных частей можно разделить фигуру, изображённую на рисунке? Количество шестиугольников и расположение в каждой фигуре должно быть одинаковое.

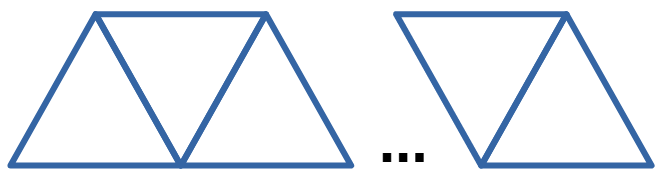
Петя из 21 спички сделал треугольник. Аня разобрала его и потратив все спички сложила полоску из треугольников. Сколько треугольников получилось?

Как-то раз Лиза и две ее подружки вышли погулять. Каждая девочка держала на руках своего питомца. Определите, как зовут девочку, у которой живет крысёнок, если известно, что: Вика выше Маши, Маша любит носить шляпки и не любит крыс, а девочки с крысенком и котенком стоят не рядом.