Задания 1-го тура XVIII олимпиады по математике для 6 класса
1 тур XVIII олимпиады по математике прошел с 16 по 29 июня 2025 г.
Задачи олимпиады
Задача №1
Вася поехал на машине в другой город по навигатору. При использовании навигатора Васин телефон полностью разряжается за 5 часов. Пока Вася едет, навигатор всегда включён, и только на время остановок Вася выключает телефон и ставит телефон на зарядку. Телефон полностью заряжается за 2 часа. Когда Вася выехал из дома, телефон был полностью заряжен, а когда он через 9 часов приехал в другой город, оставалось 25% заряда. Сколько времени Вася находился за рулем (телефон заряжается и разряжается равномерно)?
А) 7 часов Б) 7,5 часов В) 7 часов 45 минут Г) 8 часов Д) Другой ответ
Евдокимов М.А.
Задача №2
На рисунке показана фигура «почтикуб». Как могла бы выглядеть развёртка «почтикуба»?
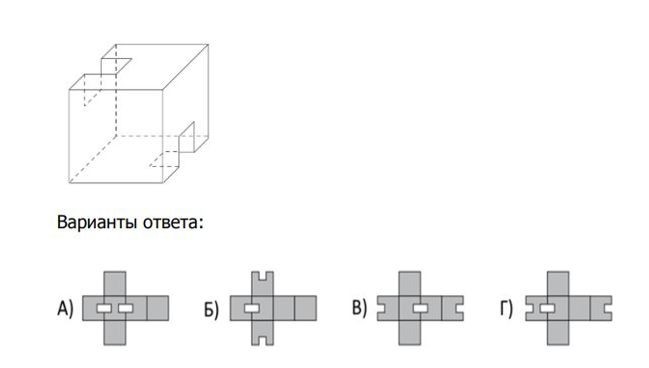
Галиулина В.Н.
Задача №3
В магазине, который закупает одинаковые кроссовки у поставщика оптом и продает их в розницу, идет акция: при покупке двух пар обуви — скидка 10%, а при покупке трех пар — скидка 20% на эту покупку. Какая наценка у магазина в процентах (на сколько процентов розничная цена больше закупочной), если магазин имеет одинаковую прибыль с каждой продажи со скидкой. Ответ дайте в процентах, округлив до ближайшего целого.
А) 25% Б) 33% В) 50% Г) 67% Д) 75%
Евдокимов М.А.
Задача №4
На школьной доске было написано неверное равенство 1 + 2 + 3 + … + 20 = 21 + 22 + 23 + … + 40 (с каждой стороны по двадцать слагаемых). Какое наименьшее количество плюсов нужно заменить на минусы, чтобы равенство стало верным? (Скобки использовать нельзя.)
А) 5 Б) 6 В) 7 Г) 8 Д) Это сделать нельзя
Евдокимов М.А.
Задача №5
У Васи было поровну четырехугольников и треугольников. Каждый четырехугольник он разрезал на 2 треугольника, а каждый треугольник — на треугольник и четырехугольник. А затем снова сделал тоже самое с новыми фигурками. В итоге у него получилось 50 треугольников. А сколько получилось четырёхугольников?
А) 50 Б) 25 В) 30 Г) 10
Манжина О.А.
Задача №6
Сколько существует пар трехзначных чисел, которые получаются друг из друга перестановкой цифр? Пары, отличающиеся порядком чисел (например (324, 243) и (243,324)) мы считаем одной и той же.
А) 1260 Б) 1701 В) 1800 Г) 2250
Манжина О.А.
Задача №7
Пять девушек бежали наперегонки. Первой начала Оля, за ней Катя, затем Амина, затем Соня и, наконец, Маша. Всякий раз, когда девушка обгоняла другую девушку, ей начислялся 1 балл. Соня финишировала первой, затем Катя, затем Оля, затем Маша и, наконец, Амина. Какое наименьшее общее количество баллов можно было бы получить?
A) 9 Б) 8 В) 6 Г) 5
Галиулина В.Н.
Задача №8
В 190 мл горячего чая добавили 10 грамм сахарного сиропа, после чего чай разбавили 50 мл холодной воды. На сколько процентов содержание сахарного сиропа в чае уменьшилось после того, как его разбавили холодной водой?
А) 1% Б) 2% В) 3% Г) 4%
Миронов Д.Р
Задача №9
Петя выложил в ряд девять коробок. В двух из них лежат синие шарики, в трёх — красные и ещё в четырёх — зелёные. Он помнит, что цвета шариков в соседних коробках различаются и что во второй и шестой коробках шарики красные, а в восьмой — не зелёный, а в первой — синий. Сколько коробок ему нужно открыть, чтобы гарантированно понять, где лежат все три красных шарика?
А) 0 Б) 1 В) 2 Г) 6
Галиулина В.Н.
Задача №10
Настя взяла дробь 5/53 и за один ход прибавляет к её числителю и знаменателю по единице. Дробь с каким значением она не сможет получить через несколько таких ходов?
А) 1/5 Б) 3/5 В) 1/6 Г) 1/7
Тодоров Е.И.
| Задача № | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Ответ | Б | В | Г | Б | В | Б | Г | А | Б | В |
I тур: 15 сентября - 27 сентября 2026
II тур: 25 октября 2026
Олимпиада по математике
Двадцать первая международная
Участвуйте в очередной математической олимпиаде от Систематики! Олимпиада проходит в два тура, по итогам которых победители получают ценные призы грамоты и дипломы.
Регистрация участника
Бесплатно


