Задания Четырнадцатой Олимпиады по математике Осень 2023 1 тур 6 класс

Задача №1.
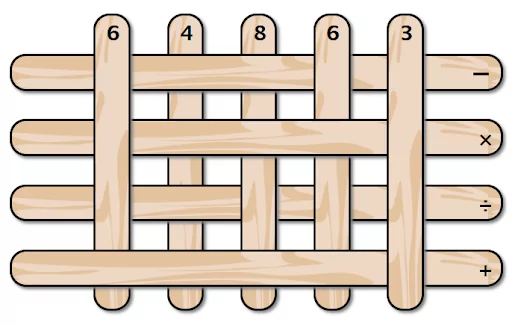
У вас есть набор палочек лежащих в виде сетки. Вы забираете палочки по одной начиная с самого верха. Чему будет равно значение полученное выражение? Пожалуйста, не забывайте про порядок действий. В ответ введите число.

Задача №2.
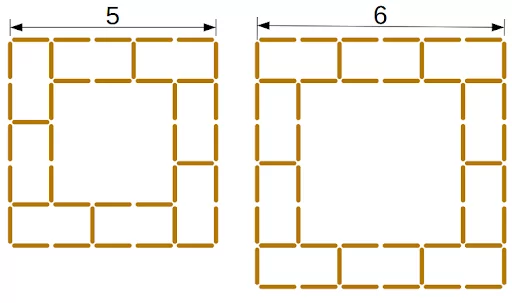
Лёша складывает из спичек фигуру по образцу (см. рис).

Сколько спичек придётся потратить на фигуру со стороной равной 14?

(А) 126
(Б) 130
(В) 134
(Г) 138
(Д) 142

Задача №3.
В городе Глупов каждый остров соединен мостами по крайней мере с третью остальных островов. На каком минимальном количестве островов может стоять город, если мостов не более 54?

(А) 16
(Б) 17
(В) 18
(Г) 20
(Д) 24

Задача №4.
На фабрике произвели по 120 перчаток трех разных размеров. И правых, и левых всех размеров — по 180 штук. Какое максимальное количество нормальных пар перчаток гарантированно можно составить из этих 360? В нормальной паре есть как левая, так и правая перчатка и их размеры одинаковы. Все левые, и все правые перчатки одного размера одинаковы.

(А) 30
(Б) 60
(В) 90
(Г) 120
(Д) 240

Задача №5
Сколько существует нечетных трехзначных чисел с произведением цифр 18?

(А) 6
(Б) 9
(В) 8
(Г) 10
(Д) 12

Задача №6.
У Таи есть два прямоугольника с целыми длинами сторон. Она заметила, что площадь первого численно равна периметру второго, а площадь второго численно равна периметру первого. Площадь одного из прямоугольников равна 54. Чему может быть равна площадь второго?

(А) 182
(Б) 110
(В) 121
(Г) 108

Задача №7.
Софья Васильевна больше всего в жизни любит математику, своих внуков и печь пирожки. Однажды к ней приехали её внучата, и чтобы побаловать их, она решила испечь много-много пирожков и сложить их на большой поднос. Наблюдательная Софья Васильевна заметила, что если каждый внук возьмёт по одному пирожку, то на подносе их останется 49, а если бы каждый внук, наоборот, положил по одному пирожку на поднос, то их стало бы 63. Сколько пирожков достанется каждому внуку, если они поровну разделят пирожки между собой?

(А) 6
(Б) 7
(В) 8
(Г) 9

Задача №8.
Матвей выписал в порядке возрастания все пятизначные числа, состоящие из цифр 1, 2, 3, 4, и 5, взятых по одному разу. На каком месте оказалось число 32451?

(А) 24
(Б) 56
(В) 58
(Г) 63

Задача №9.
Францишек взял несколько листов бумаги, сложил их пополам, вложил один в другой, сшил посередине и получил небольшую книжку. Каждую страницу он пронумеровал по порядку, начиная с номера 1 на титульной странице. Францишек заметил, что сумма четырёх номеров, написанных на внешнем листе, равна 50. А чему равна сумма номеров всех страниц в полученной книжке?

(А) 300
(Б) 450
(В) 600
(Г) невозможно определить

Задача №10.
На одной чаше весов лежит гирька весом 23 грамма. У Кати есть набор гирек весом 1, 2, 3, 4, 5, … грамм. Катя достаёт гирьки в порядке увеличения веса и кладёт их на какую-то из чаш. Какое минимальное количество гирек должна достать Катя, чтобы чаши пришли в равновесие?

(А) 6
(Б) 7
(В) 8
(Г) 9