Задания 1-го тура XIХ олимпиады по математике для 8 класса

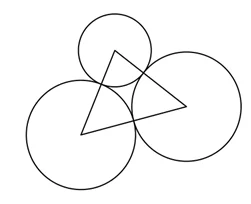
Три окружности с радиусами 2, 3 и 3 касаются друг друга. Какова площадь треугольника, образованного соединением центров этих окружностей?

Школьный турнир по футболу с участием 8 команд проходил в один круг (каждая команда играет с каждой один матч). Каждый день проводили ровно один матч. Через какое наименьшее число дней могло оказаться, что все команды набрали разное число очков к этому моменту (за победу даётся три очка, за ничью - одно)?

Иван Иванович работает в офисе на 50-м этаже небоскрёба. Лифт с 1-ого этажа до 50-ого ехал со скоростью 1 этаж в секунду, но останавливался на 10 секунд, чтобы забрать пассажиров, на каждом этаже, номер которого делится на 4 или на 5. Сколько времени заняла дорога до офиса на этом лифте у Ивана Ивановича?

Три пирата играли в кости. Вначале у всех было поровну монет. Потом первый выиграл у второго половину его денег, затем второй у третьего половину его денег, затем третий у первого половину его денег. Затем ситуация повторилась (первый выиграл у второго половину его денег, затем второй у третьего половину его денег, затем третий у первого половину его денег). После чего у одного из пиратов оказалось 72 монеты. А сколько было у двух других вместе? Число монет у игроков после каждой игры целое.

При составлении автомобильных номеров в России используется следующее правило: в начале идёт одна заглавная буква, далее три цифры (скажем, что возможны абсолютно любые комбинации, даже три нуля). После чего идут две заглавные буквы и номер региона (сегодня это нам не понадобится). Назовём "красивыми" такие номера, где одинаковы либо все буквы, либо все цифры, либо и то, и другое сразу. Какое количество комбинаций "красивых" номеров может существовать? Буквы, которые можно использовать при составлении номера представлены ниже (после олимпиады можете подумать, почему только эти буквы можно использовать): А, В, Е, К, М, Н, О, Р, С, Т, У, Х.

Сколькими способами числа от 1 до 10 (разумеется, взятые по одному разу) можно разбить на пять пар так, чтобы в каждой паре меньшее число было хотя бы вдвое меньше большего?

Снято с зачета

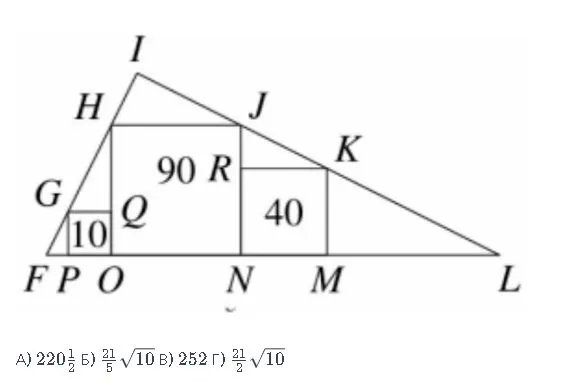
Внутри квадратов записаны их площади. Какова площадь треугольника, внутри которого они находятся?

Про натуральное число n известно, что НОК (n,12)=84 НОД(n,21)=7. Найдите сумму цифр числа n.