Задания 2-го тура XIХ олимпиады по математике для 9 класса
2 тур XIХ олимпиады по математике прошел 26 октября 2025 г.
Задачи олимпиады
Задача №1
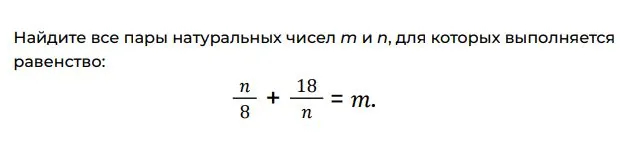
Евгений Тодроров
Задача №2
В квадрате провели четыре окружности с центрами в вершинах и радиусами равными стороне квадрата. В образовавшиеся фигуры вписаны 5 кругов. Что больше: площадь зелёного круга или сумма площадей четырёх красных? Во сколько раз?
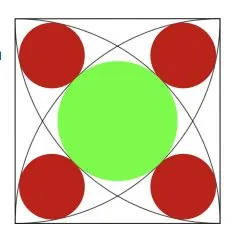
Михаил Евдокимов
Задача №3

Борис Булавинов
Задача №4
Верно ли, что, если прямоугольник можно разрезать на четыре не обязательно различных квадрата с целыми сторонами, то такой набор квадратов является единственным для данного прямоугольника? (разумеется, порядок квадратов в наборе не важен, а разрезания, отличающиеся поворотом или симметрией, будут давать одинаковые наборы)
Евгений Тодроров
Задача №5

Евгений Тодроров
Задача №6
В волшебном лесу живут эльфы и феи, которые постоянно ссорятся. Но в День начала осени короли Оберон собирает их на одной полянке круглой полянке. В этом году сказочные создания решили поступить по-умному и разделить места для танцев эльфов и фей так, чтобы они не встречались и не ссорились. Для этого круглую полянку разбили на две части, проведя диаметр AB, на нём выбрали произвольную точку D, а от неё восстановили перпендикуляр DE до точки E на крае полянки. Построили полукруги с диаметрами AD и DB, и вся часть полянки выше этих полукругов (на рисунке выделена красным) досталась феям. А эльфам достался круг, диаметром которого является отрезок DE (на рисунке выделен синим). Кому досталось больше больше места для танцев в этот День начала осени: эльфам или феям?
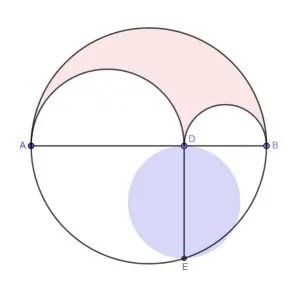
Евгений Тодроров
Задача №7

Евгений Тодроров
I тур: 15 сентября - 27 сентября 2026
II тур: 25 октября 2026
Олимпиада по математике
Двадцать первая международная
Участвуйте в очередной математической олимпиаде от Систематики! Олимпиада проходит в два тура, по итогам которых победители получают ценные призы грамоты и дипломы.
Регистрация участника
Бесплатно



