VI олимпиада по математике прошла 26 января 2020 года.
Задачи олимпиады
Задача №1
Разделите на три одинаковые фигуры по линиям сетки двумя способами.
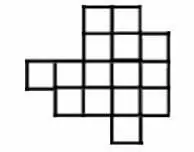
Задача №2
Катя вырезала из картона пятиугольник. А Вася вырезал четырехугольник. Они приложили один многоугольник к другому. Какое самое маленькое количество углов могло получиться у новой фигуры?
Задача №3
Мама разложила 19 яблок в три корзины. Пришёл Петя и сосчитал яблоки в двух корзинах.
"В одной корзине в три раза больше яблок”, - сказал Петя.
Пришла Катя и тоже сосчитала яблоки в двух корзинах.
"В одной корзине в четыре раза меньше яблок”, - сказала Катя.
Сколько яблок в каждой корзине?
"В одной корзине в три раза больше яблок”, - сказал Петя.
Пришла Катя и тоже сосчитала яблоки в двух корзинах.
"В одной корзине в четыре раза меньше яблок”, - сказала Катя.
Сколько яблок в каждой корзине?
Задача №4
Пиццу разрезали на равные кусочки. Оказалось, что все кусочки можно поделить поровну на двоих, на троих, на четверых, на пятерых и на шестерых. На какое самое маленькое количество кусков могли порезать пиццу?
Задача №5
Расставь числа 1,2,3,4,5,6,7,8 в кружки, чтобы сумма чисел вдоль всех линий была одинаковой. Круг тоже линия. Каждое число можно использовать только один раз.
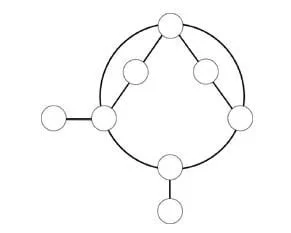
Задача №6
Соедини все точки 4 прямыми отрезками, не отрывая карандаша от бумаги.

Задача №7
Как-то все математики земли собрались вместе. Кого среди них больше: тех, у кого живёт домашнее животное или тех, кто умеет играть в шахматы и имеет кота?
Задача №8
В слове СИСТЕМАТИКА каждую букву заменили цифрой или знаком сложения.
(Одинаковыми буквами обозначены одинаковые цифры или знак сложения, разными – разные)
Могло ли в результате получиться 1000? Если да, приведите пример.
(Одинаковыми буквами обозначены одинаковые цифры или знак сложения, разными – разные)
Могло ли в результате получиться 1000? Если да, приведите пример.
I тур: 15 сентября - 27 сентября 2026
II тур: 25 октября 2026
Олимпиада по математике
Двадцать первая международная
Участвуйте в очередной математической олимпиаде от Систематики! Олимпиада проходит в два тура, по итогам которых победители получают ценные призы грамоты и дипломы.
Регистрация участника
Бесплатно


