Задания Четырнадцатой Олимпиады по математике Осень 2023 2 тур 2 класс

Задача №1.
Автор: Тодоров Евгений

Чёрт сказал кузнецу, что подарит ему черевички для невесты, если кузнец сможет двумя ударами меча разрубить подкову на 7 частей.
Помогите кузнецу выполнить это задание.

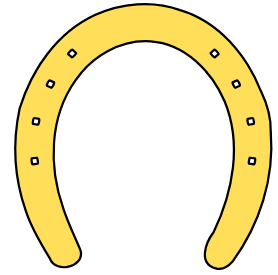
Задача №2.
Автор: Тодоров Евгений

Стакан имеет высоту 9 сантиметров. Если вставить один стакан в другой, то верхняя часть внутреннего стакана будет торчать над нижним стаканом на 2 сантиметра. Какой высоты будет «башенка» из шести таких стаканов, вставленных друг в друга?

Задача №3.
Автор: Галиулина Варвара

Разрежьте фигуру по линиям сетки на 4 одинаковых части.

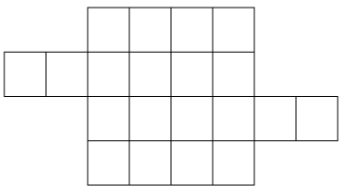
Задача №4.
Автор: Галиулина Варвара

У Васи есть несколько фигур.
Они могут быть двух цветов (зеленые и оранжевые), форм (круглые и квадратные) и типов (заполненные и пустые).
Он хочет убрать несколько фигур так, чтобы все оставшиеся были либо одного цвета, либо одной формы, либо одного типа.
Какое наименьшее количество фигур он должен убрать? Объясните почему.

Задача №5
Автор: Гусихина Екатерина

В этом примере под звездочками спрятались разные цифры. Восстановите пример.

5* + **3 = **01

Задача №6.
Автор: Галиулина Варвара

Вера учит обезьянку Анфису грамоте.
Анфиса несколько раз написала слова БОК и КОЛОБОК. Вера подсчитала, что букв О Анфиса написала на 14 больше, чем букв Б. Сколько раз было написано слово КОЛОБОК?

Задача №7.
Автор: Галиулина Варвара

В ребусе А — Б + В — Г + Д = 5 различными буквами обозначены разные цифры, при этом, каждая из них больше 0, но не больше 5. Какой цифре от 1 до 5 не может равняться Б? Почему?

Задача №8.
Автор: Галиулина Варвара

У Глупого Короля на службе состоят четыре стражника и Гениальный Сыщик.
Король отправил сыщика на разведку, чтобы тот узнал, находится ли сейчас Трубадур в городе.
Сыщик разыскал Трубадура и доложил об увиденном Первому Стражнику.
Тот доложил Второму, Второй — Третьему, Третий — Четвертому, а Четвертый Стражник сказал Королю следующее:
“Третий Стражник сказал, что Второй Стражник сказал, что Первый Стражник сказал, что Сыщик сказал, что Трубадур сейчас не в городе”.
Должен ли Король опасаться Трубадура, если ровно половина стражников — лжецы, а Сыщик всегда говорит правду?