Задания Одиннадцатой Олимпиады по математике Осень 2022 2 тур 4 класс

На данной страницы размещены олимпиадные задания с решением для 4 класса.
Олимпиада по математике прошла 23 октября 2022 года

Cкачать задание в формате PDF

Посмотреть ответы на все задания олимпиады

Задание №1

Незнайка загадал три числа, каждое из которых содержит ровно 2 единицы и, возможно, какое-то количество нулей (то есть в числе может нулей не быть вовсе). Когда он сложил эти числа, у него получилось 2022. Напишите эти числа в порядке возрастания.
(Кроме нулей и единиц, других цифр в числах нет)

Задание №2

Автор: Новодворская Ели завета

На какое наибольшее число прямоугольников, состоящих из разного числа клеток, можно разделить квадрат 4х4 по линиям сетки?

Задание №3

Автор: Новодворская Ели завета

У Ульяны пять тарелочек: голубая, розовая, желтая, салатовая и оранжевая. Она поставила их в ряд и положила на них вишенки. Справа от желтой — всего 19 вишенок, справа от сиреневой – 6, слева от голубой 18 вишенок, слева от розовой 5, а слева от сиреневой – 15, слева от оранжевой – 11. В каком порядке стоят тарелочки и сколько вишенок на каждой?

Задание №4

Автор: Новодворская Ели завета

Решите ребус, где разные буквы обозначают разные цифры, а одинаковые буквы обозначают одинаковые цифры, и за буквой О спрятался ноль:

О + ЛЛЛЛ + ИИИ + ММ + П = 9577

Задание №5

Автор: Новодворская Ели завета

У Матвея 5 пар перчаток, причем среди правых перчаток 4 – шерстяные, а среди левых перчаток 4 – черные. Пара красных шерстяных перчаток оказалась намокшей, поэтому Матвей решил надеть другие, кожаные. Какого они были цвета?

Задание №6

Автор: Мартынов Вадим

Баба-Яга собрала в саду 4 красных, 5 жёлтых и 6 зелёных яблок. Но оказалось, что среди красных и жёлтых — 7 червивых яблок, среди жёлтых и зелёных — 8 червивых яблок, среди зелёных и красных — 9 червивых яблок. Сколько из собранных Бабой-Ягой яблок оказались хорошими?

Задание №7

Автор: Иванюк Екатерина

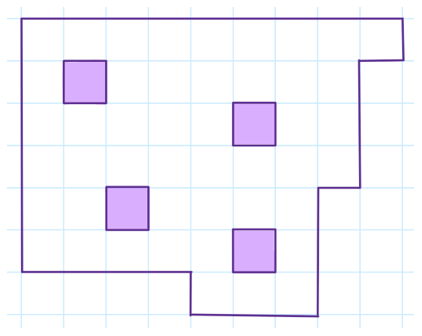
Из листка бумаги, в котором закрашенные клетки — это отверстия (см. рисунок), по линиям клеток Юра вырезал несколько букв. Напишите, какое слово могло получиться у Юры? Как могли располагаться буквы на листе, если обрезков не осталось?

Задание №8

Автор: Данченко Оксана

Вася из страны НЕЧЕТ, в которой ходят (используются) только монеты в 1, 3, 5, …, 99 рублей, приехал в страну ЧЕТ, где ходят (используются) только монеты в 2, 4, 6, …, 98. У Васи было по одной монете каждого нечетного номинала, он решил обменять их на четные монеты. Банк меняет только несколько иностранных монет на одну местную. Какое наименьшее число нечетных монет у него может остаться после нескольких таких обменов, если курс обмена 1 к 1.