Задания Двенадцатой Олимпиады по математике Зима 2023 2 тур 4 класс

Задача №1.

Автор: Галиулина Варвара

Во дворе ребята играют с котятами. Оказалось, что ног и лап в общей сложности втрое больше, чем носов.
Кого больше, котят или ребят?

Задача №2.

Автор: Галиулина Варвара

Назовем дату палиндромом, если она не поменяется при записи без точек задом наперед. Например, 01.02.2010 – палиндром (записываем без точек, получаем 01022010). Сколько таких дней еще будет в этом столетии (сейчас 2023 год)?

Задача №3.

Автор: Галиулина Варвара

В ребусе ПОП * СОС = ПОТОП каждая буква обозначает цифру от 0 до 9. Одинаковые буквы соответствуют одинаковым цифрам, разные – разным.
Найдите все решения ребуса и докажите, что других нет.

Задача №4.

Автор: Галиулина Варвара

На картинке изображена выкройка сапога. У Ухти—Тухти есть клетчатая ткань 5×5 клеток. Может ли она разрезать ее на выкройки нескольких сапог, так, чтобы лишней ткани не осталось, если резать можно только по линиям клеток?
(Выкройка– это шаблон, по которому детали одежды наносятся на ткани перед вырезанием.)

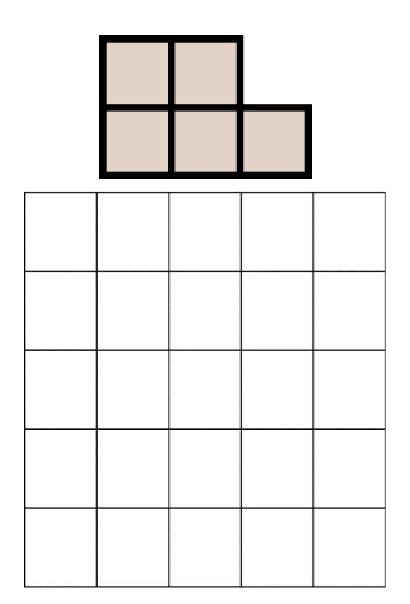
Задача №5

Автор: Галиулина Варвара

Рома загадал двузначное число, затем отнял от него произведение его цифр, какой наименьший результат он мог получить?

Задача №6.

Автор: Галиулина Варвара

Волшебник страны ОЗ выписал в ряд числа от 1—го до 6—ти. Каждую минуту он выбирает из этого ряда три числа. В результате его колдовства, к первому числу прибавляется разность второго и третьего, ко второму – разность третьего и первого, к третьему – разность первого и второго. Может ли Волшебник через несколько минут получить 6 одинаковых чисел?

Задача №7.

Автор: Галиулина Варвара

Однажды Павел Донатович решил устроить за один урок три контрольные по физике. При этом он великодушно не поставил никому три кола, однако каждый ученик получил кол хотя бы за одну контрольную. После этого директор школы приказал дать возможность всем детям исправить все их колы. Докажите, что учитель сможет рассадить учеников на переписывании по двое за парту так, чтобы соседи не могли друг у друга списывать.

Задача №8.

Автор: Тодоров Евгений Игоревич

Ученики некоторой школы должны ходить на уроки семь дней в неделю, но на самом деле иногда им лень, и они остаются дома. Известно, что в понедельник в школу пришло больше всего людей — 10, а в воскресенье меньше всего — 7. А в конце недели выяснилось, что каждый ученик класса прогулял по два школьных дня. Сколько человек учится в этом классе?