Пробная олимпиада
Задания 2-го тура XI олимпиады по математике для 5 класса
2-ой тур XI олимпиады по математике прошел 23 октября 2022 года.
Задача №1
Решите ребус, где разные буквы обозначают разные цифры, а одинаковые буквы обозначают одинаковые цифры, и за буквой О спрятался ноль:
О + ЛЛЛЛ + ИИИ + ММ + П = 9577
Задача №2
Удалите одну клеточку, а после этого разделите фигуру по линиям сетки на три равные части. Части считаются равными, если их совместить при наложении друг на друга, при этом их можно переворачивать и поворачивать.
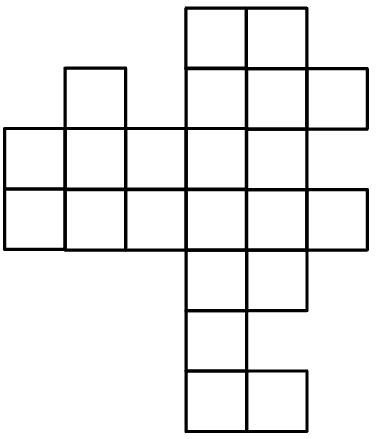
Задача №3
У гномов есть наборы с фигурками двух видов. У Балина есть фигуры вида ○ и ⌂; у Двалина — фигуры ◊ и ○; у Оина — ◊ и □; и наконец, у Глоина — фигуры ⌂ и □. Все вместе начали выкладывать красивый орнамент ⌂◊□○⌂⌂, ни один из гномов не выложил ни две соседние фигуры, ни две фигуры, стоящие через одну. Какую из фигур кто из них использовал?
Задача №4
В честь 125 годовщины окончания терраформирования Марса на стадионе Элизиум Планития прошли соревнования по взрывфутболу. Каждая из команд взрыв-футболистов состоит из восьми моделей взрыв-роботов: шесть в основном составе и две в дополнительном. Каждый матч длился ровно 60 минут. В финале в одной из команд обе модели роботов из дополнительного состава заменяли каждую из шести основных моделей так, что все восемь типов взрыв-роботов находились в игре одинаковое время. Найдите это время, если известно, что в любой момент игры на поле находилось ровно шесть “футболистов”.
Задача №5
В клетках квадрата 3х3 записаны цифры 1,2,3,4,5,6,7,8,9. Могло ли так оказаться, что среди шести трёхзначных чисел, написанных в столбцах сверху вниз и в строках слева направо, были такие: 452, 689, 173, 538?
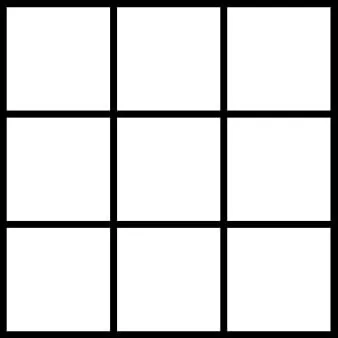
Задача №6
Вася из страны НЕЧЕТ, в которой ходят (используются) только монеты в 1, 3, 5, ..., 99 рублей, приехал в страну ЧЕТ, где ходят (используются) только монеты в 2, 4, 6, ..., 98. У Васи было по одной монете каждого нечетного номинала, он решил обменять их на четные монеты. Банк меняет только несколько иностранных монет на одну местную. Какое наименьшее число нечетных монет у него может остаться после нескольких таких обменов, если курс обмена 1 к 1.
Задача №7
В детском саду устраивается утренник. Дети, одетые в костюмы помидоров и баклажанов, водят хоровод. В некоторый момент каждый из них сказал своему соседу справа: “Я - помидор” или “Я - баклажан”. Известно, что “помидоры” “помидорам” сказали правду, а “баклажанам” соврали, а “баклажаны” “баклажанам” сказали правду, а “помидорам” соврали. Так же известно, что “баклажанов” было 13, а “помидоров” – 12. Сколько фраз: “Я – баклажан” могло быть сказано?
Задача №8
В очереди в школьную столовую стояли 30 школьников. Первой в очереди стояла Аня, последним в очереди был Витя. В некоторый момент между каждыми двумя рядом стоящими мальчиками встало по мальчику, а между каждыми двумя рядом стоящими девочками – по девочке. Могло ли оказаться, что теперь в очереди стоят 45 школьников?
Решения и ответы

Пройдите пробную олимпиаду по математике для 1–9 классов.
1-й тур: 15 – 29 сентября
2-й тур: 20 июля
Олимпиада по математике
Девятнадцатая международная олимпиада по математике
Участвуйте в очередной математической олимпиаде от Систематики! Олимпиада проходит в два тура, по итогам которых победители получают ценные призы грамоты и дипломы.
Зарегистрироваться
Бесплатно


