Задания X олимпиады по математике для 5 класса

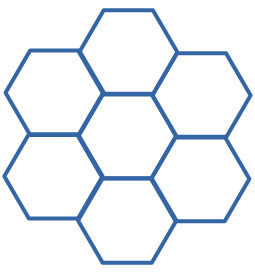
В клетках гексагональной сетки стоят жители острова рыцарей и лжецов. Задания Десятой Олимпиады по математике Зима 2022 5 класс В некоторый момент каждый из них произнес: «Во всех соседних со мной клетках стоят лжецы». Сколько рыцарей могло быть среди них? (приведите все возможные варианты и докажите, что других нет) (Примечание: Каждый обитатель этого острова является либо рыцарем, либо лжецом. Рыцари всегда говорят правду (то есть высказывают только истинные утверждения), лжецы всегда лгут (то есть их высказывания всегда ложны).)

Население Москвы (по имеющимся данным) составляет более 12,5 млн. человек, а площадь примерно 2500 км2. Как вы думаете, смогли бы все жители Москвы, взявшись за плечи, встать в хоровод вокруг фигуры (любой удобной для расчета формы) с площадью равной площади Москвы? Ответ подтвердите расчетом. Недостающие данные можно взять из соображений логичности.

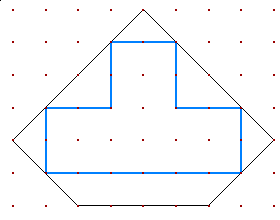
Вокруг дома в виде буквы «Т» построили забор, как показано на рисунке. В каком соотношении делятся площади под домом и двора внутри забора? Ответ дать в виде несократимой дроби, где числитель — доля двора, а знаменатель доля площади дома. В решении пояснить свой ответ.

Коля взял набор из 10 кубиков и начал собирать из них фигуру, склеивая их по граням (склеиваемые грани приклеиваются друг к другу полностью). Коля сказал брату, что хочет на каждую грань кубиков, которые видны (т. е. не склеены с другой гранью) приклеить красивую маленькую наклейку. Брат подарил ему 3 набора по 5 наклеек и 4 набора по 6. Сможет ли Коля осуществить свою задумку используя все наклейки полностью, если нельзя оставлять не оклеенных граней кубиков и нельзя клеить наклейки на одну грань больше 1 раза?

Существует ли такой прямоугольник, у которого значение периметра в см вдвое больше значения площади в квадратных см?

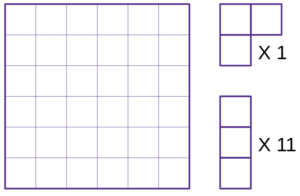
Можно ли разрезать квадрат 6х6 на 1 “уголок из трех клеток” и 11 фигурок “полоска из трех клеток”? Фигурки можно поворачивать и переворачивать.

У Бильбо в каморке стояли 32 бочки с элем и медом, каждая вместимостью 5 пинт. Когда пожаловавшие в гости гномы выпили половину всего меда и половину всего эля, хозяйственный Бильбо решил перелить остатки в бутылки объемом 3 пинты. У него есть 27 таких бутылок. Точно ли ему их хватит, если смешивать напитки запрещено?

Илья купил упаковку глины (в форме кирпичика). Из части он слепил армию одинаковых гоблинов в количестве 14 штук. Остальную глину он аккуратно смял в кирпичик, который был в два раза по высоте, ширине и длине меньше купленного. Сколько еще таких же гоблинов можно было слепить из оставшегося куска?

Винни Пух взял несколько горшочков у Кролика и пошел домой, поедая мед. Пройдя четверть пути, он понял, что может есть мед в два раза быстрее и ему все равно идеально хватит меда до дома. Не дойдя четверть пути до дома, он решил вернуться за добавкой. Возвращаясь, к Кролику он ел мёд с той же скоростью, а бежал в два раза быстрее. Хватит ли ему меда до дома Кролика?

У Маши есть 7 старых альбомов, из которых уже частично вырвали страницы, в итоге страниц в сумме осталось 125. Между страницами Маша засушила по одному листочку клена. Всего было 27 красных листов, 53 желтых, остальные оранжевые. А сколько было оранжевых?