Как успешно написать олимпиаду
Курс прошли 3 000 учеников! Присоединяйтесь к подготовке
Задания 1-го тура XI олимпиады по математике для 8 класса

Только сегодня до 23:59
1 тур XI олимпиады по математике прошел 2 октября 2022 года.
Задача №1
Вычислите/упростите: (A) 43/60 (Б) 19/20 (В) 23/30 (Г) 79/120 (Д) 5/6
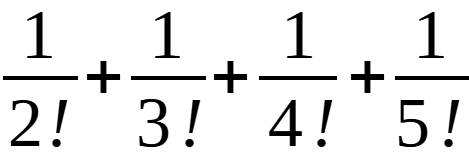
Задача №2
Даны числа: -11, -7, -2, 3, 4, 6. Выберите минимальное произведение двух из них: (A) -66 (Б) -42 (В) -6 (Г) 1 (Д) 12
Задача №3
Запишите минимальное 11-ти значное число делящееся на 72 состоящее из всех цифр минимум по 1 разу.
Задача №4
В каком веке будет больше високосных лет в 23 или 24? (A) В 23 меньше на 2 дня (Б) В 23 меньше на 1 день (В) Одинаково (Г) В 23 больше на 1 день (Д) В 23 больше на 2 дня
Задача №5
На координатной плоскости обозначили 5 точек из которых 4 оказались вершинами квадрата. Какая точка вершиной квадрата являться не может? (A) (-1;3) (Б) (0;2) (В) (1;-1) (Г) (5;1) (Д) (3;5)
Задача №6
Смешиваются 2 раствора первый содержит 15% растворённых веществ и массой 2 кг, а второй 20% и массу3 кг. Чему равно итоговое содержимое растворённых веществ если растворы можно смешивать и никакой видимой реакции не произойдёт? (A) 16,4% (Б) 17,2% (В) 18,0% (Г) 18,2% (Д) 19,0%
Задача №7
Дан куб размера NxNxN склеенный из N3 единичных кубиков (их сторона равна 1). Его поверхность покрашена в некоторый цвет. При каком значении N впервые числовая величина площади поверхности станет меньше общего количества единичных кубиков, которые вообще не имеют ни одной окрашенной стороны? (A) При N=8 (Б) При N=9 (В) При N=10 (Г) При N=11 (Д) При N=12
Задача №8
Назовём число N-годичным, если сумма его цифр равна году N. Чему равен старший разряд у самого маленького 2022-годичного числа? Введите цифру ответа:
Задача №9
Фигура Циклоп может съесть свою жертву или переместиться в новую позицию если может добраться до неё двигаясь только по 2 направлениям из четырёх по границам сетки (можно, например, совершать сколь угодно много шагов вправо и вверх, но нельзя при этом делать ни одного шага влево или вниз) Подсчитайте количество различных маршрутов для Циклопа (находящегося в т. А) позволяющих добраться до цели(в т. Б).
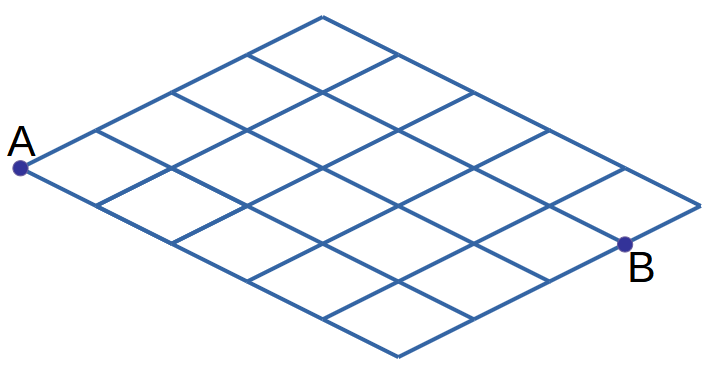
Задача №10
Коля пошел в поход из турбазы к озеру. Он хотел быть у озера точно в 19:00. За ⅔ планируемого времени он преодолел ¾ пути. Понимая, что задерживается он ускорился и добрался к озеру в 19 : 00, как и хотел первоначально. Найдите отношение скоростей на первой и последней четвертях его пути? (А) 1,25 : 1 (Б) 4 : 3 (В) 1,5 : 1 (Г) 2 : 1 (Д) 3 : 1
Задача №11
Вовочке достались странные часы – часовая стрелка у них идёт на встречу минутной, а в остальном это обычный часы с циферблатом с числами от 1 до 12. Сколько раз за сутки на них можно видеть угол между часовой и минутной стрелками равный ровно 90 градусам (сутки начинаются в 0 часов 0 минут)? (A) 22 (Б) 26 (В) 44 (Г) 52 (Д) Ни одно не подходит
Задача №12
Выполнение работ по проекту было оценено в 882 тыс. рублей на заработную плату из расчёта, что его будут выполнять (с условно одинаковой производительностью) 15 человек в течении 12 дней. К работе приступили 8 человек и проработали 7 дней. После этого к бригаде добавили 3 человек и в этом составе они проработали 6 дней. Для скорейшего завершения проекта к бригаде на 4 дня добавили ещё 6 человек. После окончания основных работ проект был показан заказчику и на устранении недостатков работало 5 людей в течении 4 дней (остальные работники были распределены на другие проекты). Дальше работа была принята и выплачена оговоренная сумма. На сколько меньше запланированного получит каждый работник в пересчёте на 1 день если всю полученную сумму разделили между всеми работниками пропорционально отработанным дням? (A) На 240 рублей меньше (Б) На 350 рублей меньше (В) На 500 рублей меньше (Г) На 700 рублей меньше (Д) На 900 рублей меньше
Задача №13
Джон никогда не говорит правды. В один прекрасный день Джон в разговоре с Кристианом воскликнул : «По крайней мере один из нас никогда не лжет» Тогда будет справедливо утверждение: (A) Кристиан всегда лжет (Б) Случается, что Кристиан лжет (В) Кристиан полностью правдив (Г) Иногда Кристиан говорит правду (Д) Джон не мог бы такое сказать
Скачать задания в формате PDF
| Вопрос № | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| Ответ | А | А | 10023457896 | Б | Б | В | Г | 6 | 56 | В | Г | Г | Б |

Пробная олимпиада
Пройдите пробную олимпиаду по математике для 1–9 классов.
1-й тур: 16 – 29 июня
2-й тур: 20 июля
Олимпиада по математике
Восемнадцатая международная олимпиада по математике
Участвуйте в очередной математической олимпиаде от Систематики! Олимпиада проходит в два тура, по итогам которых победители получают ценные призы грамоты и дипломы.
Зарегистрироваться
Бесплатно


