Задания Тринадцатой Олимпиады по математике Весна 2023 1 тур 8 класс

1 тур олимпиады по математике прошёл с 15 мая по 7 июня 2023 года

Задача №1
Игорь был приглашен на вечеринку в честь дня рождения его лучшего друга Никиты.
Живут друзья не очень далеко друг от друга — пешком расстояние от своего дома до дома Никиты Игорь преодолевает за 20 минут. Уже идя к Никите на День Рождения Игорь решил, что будет здорово взять ещё плакат от любимой Никитой игры Minecraft. Игорь знает — если зайти за плакатом, то придёт позже начала вечеринки на 10 минут, а если не заходить за плакатом с Minecraft, то он придёт за 8 минут до начала вечеринки.
Сколько процентов пути он уже успел пройти?
(А) 30%
(Б) 35%
(В) 40%
(Г) 45%
(Д) 50%

Задача №2
Машенька вырезала из квадратного листочка в клеточку квадрат меньшего размера, ровно по границам клеточек. Какого максимального размера мог быть первоначальный квадрат если остался кусочек площадью в 1961 клеточку. Введите число — сторону первоначального квадрата.

Задача №3
Площадь фигуры, образованной пересечением линий равна…

(А) 0
(Б) 1/3
(В) 2/3
(Г) 1
(Д) 4/3

Задача №4
Сумма цифр числа n равна 10. Если к сумме цифр прибавить их произведение, то получится произведение цифр числа n+1. Сколько существует таких чисел?
(А) 32
(Б) 20
(В) 9
(Г) 0
(Д) 38

Задача №5
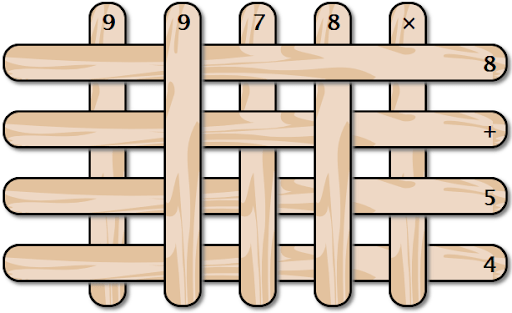
У вас есть набор палочек, лежащих в виде сетки. Вы забираете палочки по одной начиная с самого верха. Чему будет равно значение полученного выражения? Пожалуйста, не забывайте про порядок действий. В ответ введите число.

Задача №6
Расставьте в выражении цифры от 1 до 9 так чтобы получилось верное равенство. Чему равно центральное число если точно известно, что в нём нет 5?

Задача №7
Аня посмотрела на свои электронные часы и записала сумму цифр на них (часы показывают время в формате ЧЧ:ММ). Когда она взглянула на них через 8 минут, сумма цифр уменьшилась втрое. Аня решила посчитать, сколько ЧЧ:ММ в сутках обладают этим свойством. Какой ответ она получила?(A) При N=8
(А) 0
(Б) 1
(В) 4
(Г) 7
(Д) 10

Задача №8
Генри Кавилл собрал армию солдат для своей любимой настолки Warhammer 40000. Оказалось, что его армию можно построить в виде прямоугольника 64 различными способами. Чему равна численность его войск, если это минимально возможное число? Расстановка 1xN и Nx1 считаются различными.

Задача №9
В треугольнике ABC провели биссектрису CK угла ACB и биссектрису внешнего угла C. Через вершину B провели прямую l, параллельную стороне AC. Продолжение CK пересекает l в точке L, биссектриса внешнего угла – в точке M. Найти CK, если LM = 8, CM = 4, AK:KB = 3:1

Задача №10
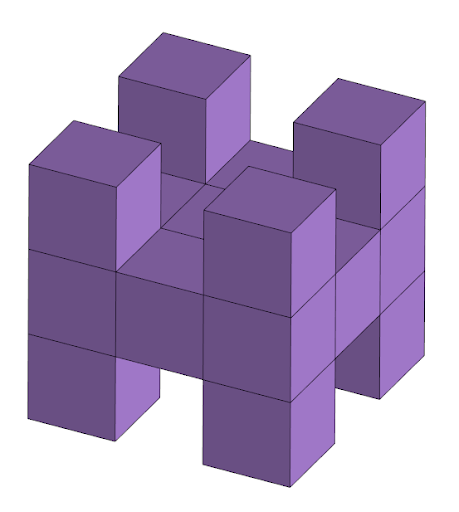
Из куба 3х3х3 вырезали несколько кубиков как показано на рисунке. Как изменилась площадь поверхности? (вырез в виде буквы “+” одинаковый сверху и снизу)

(А) Увеличилась на 9
(Б) Увеличилась на 8
(В) Увеличилась на 7
(Г) Уменьшилась на 7
(Д) Не изменилась