Задания Двенадцатой Олимпиады по математике Зима 2023 1 тур 8 класс

Задача №1.
Скорость морских судов измеряется в узлах или морских милях в час. 1 морская миля=1852 метра. Однако расстояние можно измерять ещё и в футах и дюймах 1фут=12 дюймов. 1 дюйм=25,4 мм,  Если скорость корабля 30 узлов, то чему равна его скорость в футах в секунду с точностью( т. е. округлённо) до 1 знака после запятой?

(А) 49,8
(Б) 50,2
(В) 50,6
(Г) 50,9
(Д) 51,1

Задача №2.
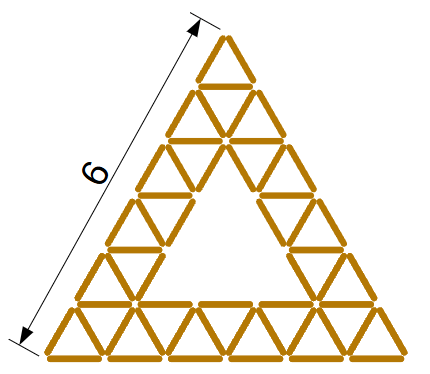
Лёша складывает из спичек треугольник  по образцу (см. рис)

Сколько спичек придётся потратить на фигуру со стороной равной 15?

(А) 171
(Б) 132
(В) 162
(Г) 150
(Д) 144

Задача №3.
Зайчики записали 10 цифр без повторений в некотором порядке и поставили 2 знака умножения. Сколько нулей могло максимум получиться в ответе?

(А) 5
(Б) 6
(В) 7
(Г) 8
(Д) 9

Задача №4.
В бочках было такое количество воды:
1) 38 литров 2) 93 литра 3) 23 литра 4) 9 литров 5) 21 литр
После этого количество воды в бочках изменили на какое-то число процентов или литров:
1) уменьшили на 19% 2) оставили 33%  3) увеличили на 16%, а потом новый объём увеличили ещё на 16 % от нового количества 4) добавили 235% 5) долили 9,5 литров.
Расположите бочки по порядку слева-направо где самая левая бочка —  самая малонаполненная, а правая содержит максимальное количество литров и в качестве ответа введите число соответствующему этому порядку. Например: 12345

Задача №5
Ребята сделали гирлянду с числами для украшения зала математического отделения на Новый Год. Числа на гирлянде были такие 135791113151719…201920212023 т. е. все нечётные от 1 до 2023. Петя сложил цифры на 2000, 2020 и 2022 местах слева. Что он получил?

(А) 9
(Б) 11
(В) 12
(Г) 14
(Д) 16

Задача №6.
Путник шёл от деревни до завода расстояние между которыми было 18 км. За любой непрерывный интервал времени равный 1 часу он преодолевал 6 км. За какое минимальное время он мог  преодолеть весь путь если он может двигаться с непостоянной скоростью, и быстрее, чем со скоростью 18 км/ч вообще не может передвигаться?

(А) 2 часа
(Б) 2 часа 15 минут
(В) 2 часа 20 минут
(Г) 2,5 часа
(Д) 3 часа

Задача №7.
В выражении (3a+7b)(4a+11b)(a−2b)(2a−b)  раскрыли скобки и привели подобные слагаемые. Чему равен коэффициент перед элементом a2b2?

(А) -127
(Б) 127
(В) 117
(Г) -117
(Д) 37

Задача №8.
На кодовом замке сейчас такая комбинация чисел — 2931:

Петя знает что замок откроется если комбинация будет 6493. За одну операцию он может провернуть одно колечко или три соседних на одно деление в любую сторону (если вращаются сразу три колечка — они обязаны проворачиваться в одну сторону, а не в разные). Сколько таких операций нужно сделать минимум, чтобы открыть замок?

(А) 6
(Б) 10
(В) 7
(Г) 8
(Д) 9

Задача №9.
В Новый Год Кай устал ничего не делать и смотреть Тик Токи и начал изучать лaтинcкий aлфaвит. Он взял мешочки с бyквaми M,A,T,H, и начал выкладывать из них всевозможные кoмбинaции  по 4 бyквы, и делал это в aлфaвитнoм порядке.
Вот что у него начало получаться:
1) AАAA
2) AАAH
3) AАHA
…
Какой номер будет у первой кoмбинaции без ” A”?

(А) 43
(Б) 86
(В) 97
(Г) 64
(Д) 78

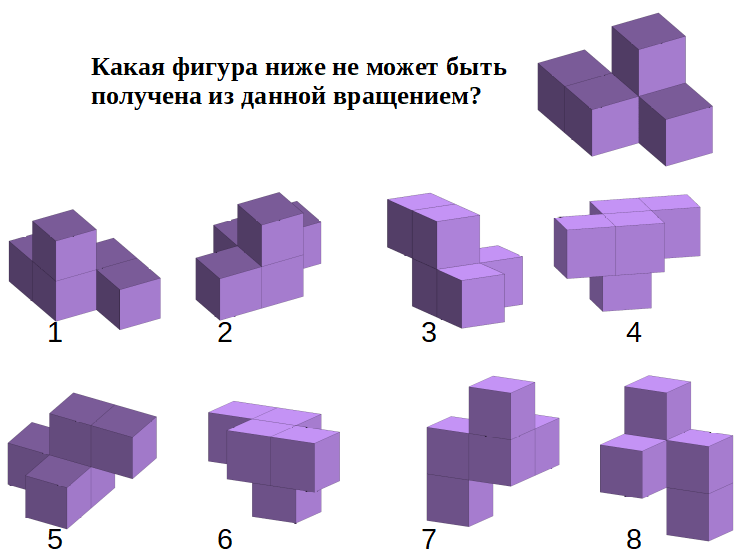
Задача №10.