Задания 2-го тура XII олимпиады по математике для 8 класса
2-ой тур XII олимпиады по математике прошел 26 февраля 2023 года.
Задачи олимпиады
Задача №1
Докажите, что синий отрезок в два раза короче красного (см. рисунок). Желтые фигуры - это правильный треугольник и правильный шестиугольник, имеющие общую вершину.
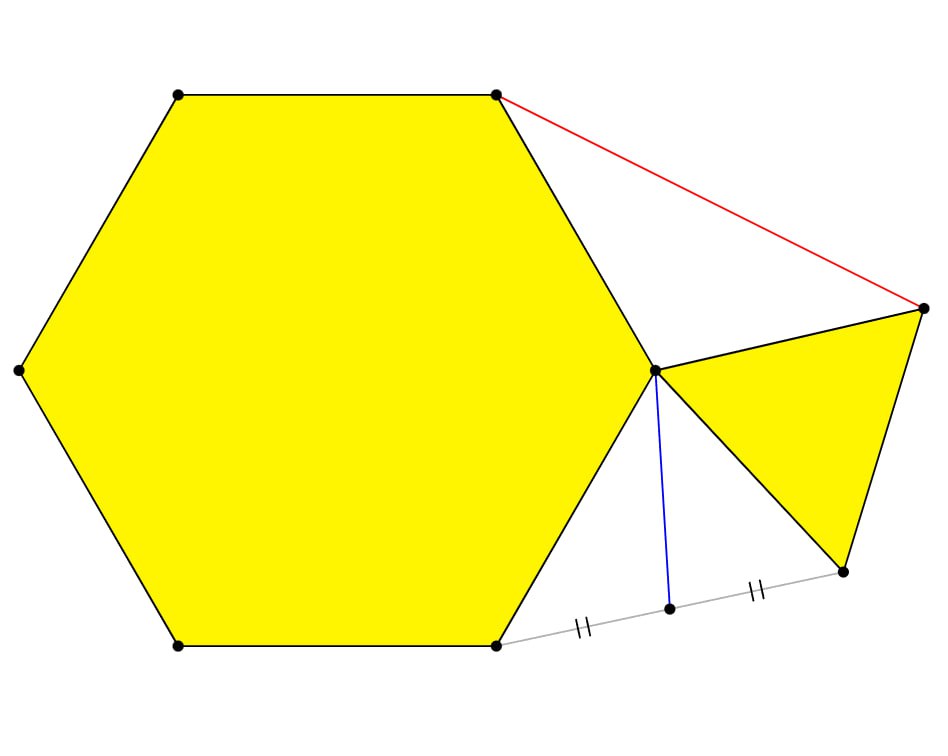
Задача №2
Можно ли представить число 10^2023 в виде суммы двух кубов натуральных чисел?
Задача №3
Маша считает, что трёхзначное число делится на 11, если работает следующее правило: цифра в центре равна сумме цифр по краям. А Саша посчитал сколько трёхзначных чисел делятся на 11, но для которых правило Маши не работает. Сколько чисел насчитал Саша?
Задача №4
Прямоугольный параллелепипед 3x5x7 составлен из кубических лампочек 1x1x1. Робот начинает передвигаться по поверхности параллелепипеда следующим образом: с лампочки, на которой он стоит, он может перейти на другую грань этой лампочки или на лампочку, смежную с ней. Если лампочка, на которую наступил робот, была выключена, то она загорается. Если лампочка была включена, то она гаснет. Если робот перемещается по граням одной и той же лампочки, она не включается и не выключается. Может ли робот зажечь все лампочки, обойдя каждую клетку по одному разу, если на момент начала движения горит только лампочка, на которой стоит робот и эту клетку посещать больше нельзя?
Задача №5
Чтобы отпраздновать постройку Дома Дружбы Чебурашка и его друзья решили устроить пир. Для этого они расставили 19 блюд на прямоугольном столе размера 1,1x1,4 метра так, чтобы от центра каждого блюда до краев стола было целое число дециметров. Блюдо представляет собой круг диаметром 20 см. Края блюд не могут выходить за границы стола. Докажите, что Чебурашка сможет уместить еще одно блюдо на столе.
Задача №6
У каждого из 333 участников научной конференции не более двух очень близких друзей. Оказавшись в одном зале, близкие друзья немедленно начинают слишком громко обсуждать свои научные исследования и срывают конференцию. Какое наименьшее число залов необходимо иметь организаторам конференции, чтобы всё прошло без срывов?
Задача №7
Про числа x, y, z известно, что И Вычислите значение суммы x+y+z.
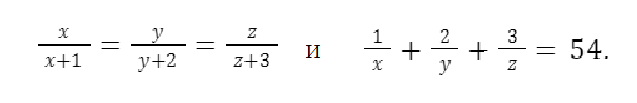
Задача №8
Доказать, что для любых положительных х1, х2, х3
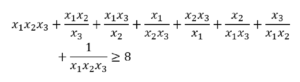
I тур: 15 сентября - 27 сентября 2026
II тур: 25 октября 2026
Олимпиада по математике
Двадцать первая международная
Участвуйте в очередной математической олимпиаде от Систематики! Олимпиада проходит в два тура, по итогам которых победители получают ценные призы грамоты и дипломы.
Регистрация участника
Бесплатно



