Задания 2-го тура XV олимпиады по математике для 3 класса
2 тур XV олимпиады по математике прошел 25 февраля 2024 года.
Задачи олимпиады
Задача №1
На своём Дне Рождения Шарлотта Ля Бафф раздала всем своим подругам по три пирожных, после чего пирожных не осталось. Но тут она спохватилась, что чуть не забыла про Тиану. Тогда она забрала пирожные обратно и раздала всем уже по два, включая Тиану, и еще четыре пирожных у нее осталось. Сколько пирожных было у Шарлотты?

Галиулина В. Н.
Задача №2
Трое лучников состязались в стрельбе по мишени. Каждый сделал по 2 выстрела. Известно, что самый меткий из них набрал больше всех очков, но не более, чем два других лучника вместе взятые. Сколько очков набрал самый слабый участник состязания?
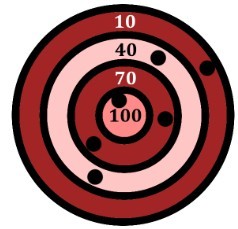
Галиулина В. Н.
Задача №3
В честь дня летнего солнцестояния все жители острова рыцарей и лжецов встали в хоровод вокруг большого костра. Каждый из них сказал: «Рядом со мной стоит лжец». Могло ли лжецов быть больше, чем рыцарей? (Напоминаем, что рыцари всегда говорят правду, а лжецы всегда говорят ложь)
Галиулина В. Н.
Задача №4
Свеча полностью сгорает за 48 минут. Эмиль может отмерить середину свечи, и перочинным ножом разделить её на две равные части. (Части тоже можно делить пополам) Сможет ли он при помощи одной свечи засечь ровно 33 минуты?

Галиулина В. Н.
Задача №5
Элемент может быть прикреплен к электросхеме четырьмя способами: Если медные проводки двух элементов соприкасаются, случается короткое замыкание (см. картинку)
Докажите, что нельзя заполнить этими элементами всю схему так, чтобы не случилось короткого замыкания.
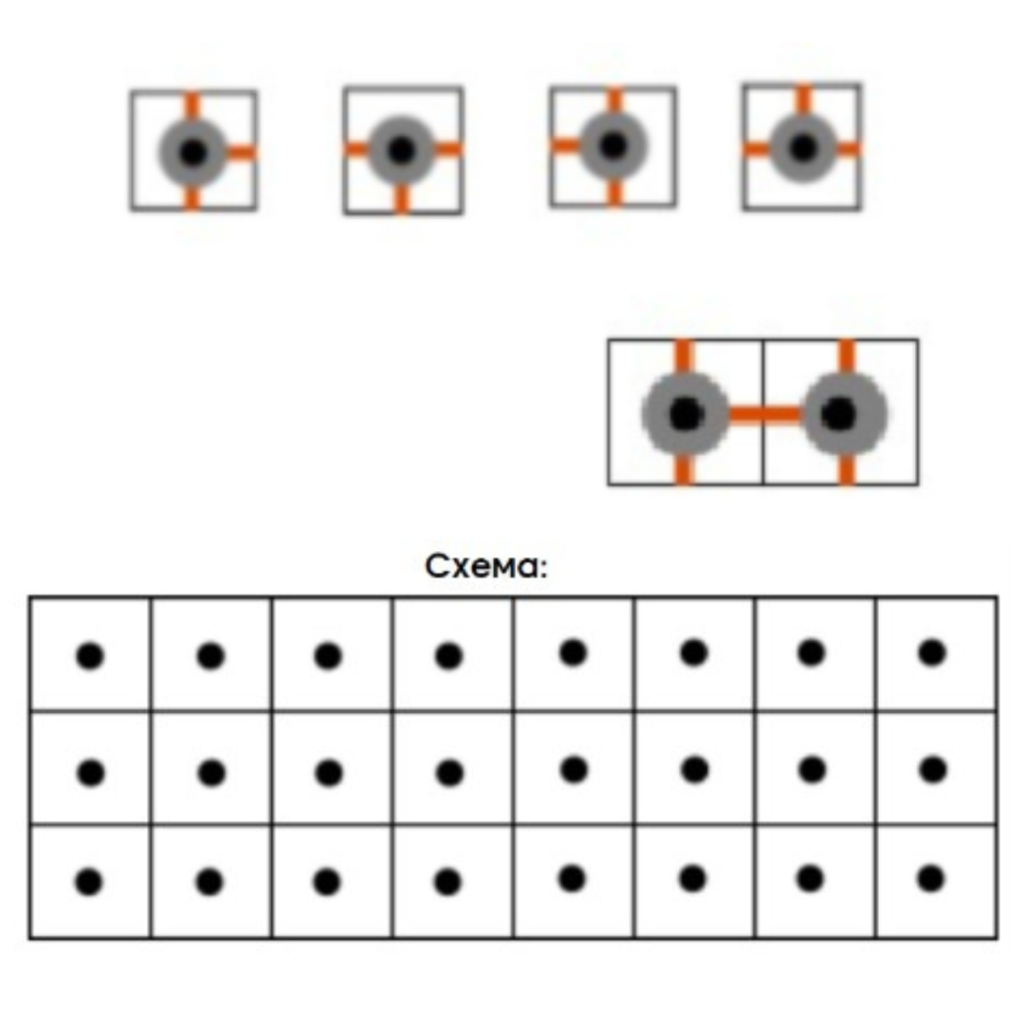
Галиулина В. Н.
Задача №6
Можно ли разрезать прямоугольник 4x5 по клеточкам на 5 попарно неравных фигур (т.е., никакие две из них нельзя совместить наложением) с одинаковой площадью? Фигуры, полученные при помощи поворота, считаются равными, а с помощью переворота (отражения) – нет.

Галиулина В. Н.
Задача №7
Франциска выбежала из дома со скоростью 7 км/ч. В 15:00 она получает на свои умные часы сообщение с напоминанием о том, что в 15:30 у нее назначена встреча с подругой. Она бежит обратно домой тем же путем с удвоенной скоростью, а затем ей требуется еще 10 минут, чтобы принять душ и переодеться. Затем она идет со скоростью 3 км/ч к своей подруге, которая живет в 250 м. от нее, и приходит вовремя. а) Сколько времени понадобится Франциске, чтобы добраться до подруги после того, как она пришла домой? б) Как далеко от дома находилась Франциска, когда она получила сообщение с напоминанием? в) В какое время Франциска начала бегать?
Иванюк Д. В.
I тур: 15 сентября - 27 сентября 2026
II тур: 25 октября 2026
Олимпиада по математике
Двадцать первая международная
Участвуйте в очередной математической олимпиаде от Систематики! Олимпиада проходит в два тура, по итогам которых победители получают ценные призы грамоты и дипломы.
Регистрация участника
Бесплатно



