Пробная олимпиада
Задания 1-го тура XIV олимпиады по математике для 3 класса
1-ый тур XIV олимпиады по математике прошел с 18 по 30 сентября 2023 года.
Задача №1
Робот Бобот умеет писать числа, а так же моментально выполняет операции сложения. Однажды Боботу дали два листочка, на левом из которых было написано число 17. Бобот решил расставить числа 1, 2, 4, 8, 16 и 32 (без повторений) на листочках так, чтобы суммы чисел на каждом листочке были одинаковыми. Где окажутся числа 4 и 8? (А) оба на левом (Б) 4 на левом, 8 на правом (В) 8 на левом, 4 на правом (Г) оба на правом
Тодоров Е. И.
Задача №2
Щенок Гав и котёнок Мяу нашли палку колбасы длиной тридцать сантиметров. Щенок Гав съел в четыре раза больше колбасы, чем котёнок Мяу. Сколько колбасы досталось котёнку Мяу? (А) 4 (Б) 6 (В) 5 (Г) 7
Гавва А. С.
Задача №3
На квадратном участке земли живут пять фермеров. Их хозяйства отделены друг от друга заборами. Фермеры считаются соседями, если между их фермами тянется общий кусочек забора. «У меня больше всех соседей», - сказал Джек. «А у меня соседей меньше всех», - ответил Том. На какой карте изображен этот участок земли?
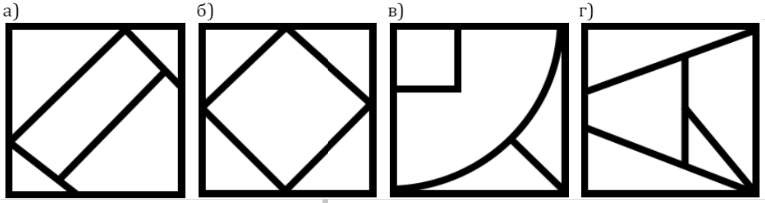
Галиулина В. Н.
Задача №4
Девочки из танцевального ансамбля захотели надеть на свое выступления однотонные юбки и однотонные футболки. Цвет футболки не должен совпадать с цветом юбки, и все девочки хотят выглядеть по-разному. Какое наименьшее количество цветов должно быть у них в одежде, если в ансамбле 23 участницы? (А) 6 (Б) 5 (В) 4 (Г) 7
Галиулина В. Н.
Задача №5
Ладья за один ход передвигается на любое количество клеток влево, вправо, вверх, или вниз. Умный мышонок по имени Элджернон решил построить «лабиринт для ладьи». За какое наименьшее количество ходов ладья доберется из клетки А в клетку Б? (А) 6 (Б) 5 (В) 9 (Г) 8
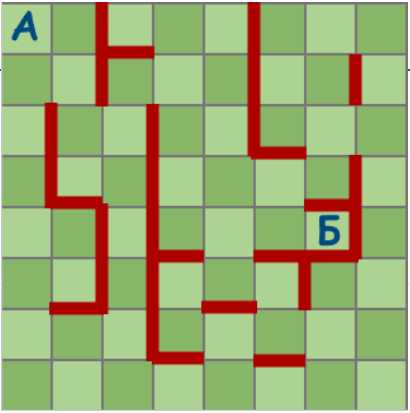
Галиулина В. Н.
Задача №6
Мастеру нужно провести интернет из города до деревни Простоквашино. Расстояние между ними 20 километров. Чтобы протянуть провод, нужно поставить столбы через каждые десять метров. Сколько столбов понадобится? (А) 1999 (Б) 2002 (В) 2001 (Г) 2000
Гавва А. С.
Задача №7
К кормушке, которую повесила Оля, прилетают только воробьи и голуби. Воробушек съедает три семечки, а голубь – пять. Оля посчитала, что во вторник к ней прилетело 17 птиц и что они съели 71 семечку. Сколько воробушек прилетело к Оле во вторник? (А) 9 (Б) 8 (В) 7 (Г) 10
Гавва А. С.
Задача №8
Пираты считали сокровища. Старший из них заметил, что если каждый из пиратов добавит к имеющимся сокровищам по мешку золота, то всего мешков станет 42, а если, наоборот, каждый из пиратов заберёт по мешку, то мешков станет 28. А сколько мешков получит каждый из пиратов, если поровну разделить имеющиеся мешки с золотом между ними? (А) 6 (Б) 4 (В) 5 (Г) 10
Тодоров Е. И.
Задача №9
Некоторые кочки на болоте в лягушачьей деревне соединены мостиками, как показано на рисунке, лягушонок Прутик может перепрыгнуть с любой кочки на любую другую, но если между ними есть мостик, то лягушонок лучше пройдет по нему. Прутик вылез из болота на ближайшую кочку. Оттуда он за один “ход” (переход или “перепрыг”) добрался до кочки под номером 4 и от нее сделал еще один ход. Известно, что Прутик один раз перепрыгнул с кочки на кочку, и один раз прошел по мостику (но в каком порядке - неизвестно). Сколькими способами он мог это сделать? (А) 2 (Б) 4 (В) 6 (Г) 8
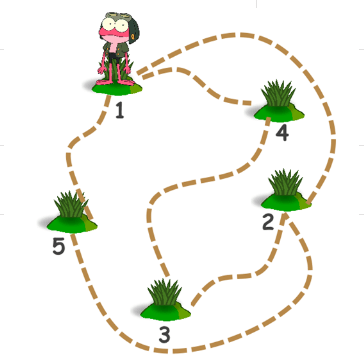
Галиулина В. Н.
Задача №10
В жилом комплексе “Кошачий” есть квартиры по одной, две и три комнаты, причём однокомнатных столько же, сколько и трёхкомнатных, а всего квартир ровно 300. Известно, что в двухкомнатных квартирах живёт по две кошки, в трёхкомнатных – по четыре, а в однокомнатных кошек нет. Сколько всего кошек живёт в жилом комплексе? (А) 300 (Б) 600 (В) 900 (Г) невозможно определить
Тодоров Е. И.
Задача №11
На стол выложены в алфавитном порядке карточки, на которых написаны буквы А, Б, В, Г, Д, Е, Ё, Ж, И и Й. На другой стороны каждой карточки написано целое число так, что сумма чисел на любых трёх подряд идущих карточках равна 16. Известно, что на другой стороне карточки в буквой А написано число 3, а на другой карточке с буквой И написано число 5. Какое число написано с другой стороны карточки с буквой Е? (А) 3 (Б) 8 (В) 5 (Г) 7
Тодоров Е. И.
| Задача № | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| Ответ | Б | Б | А | А | А | В | В | В | Г | Б | В |

Пройдите пробную олимпиаду по математике для 1–9 классов.
1-й тур: 15 – 29 сентября
2-й тур: 20 июля
Олимпиада по математике
Девятнадцатая международная олимпиада по математике
Участвуйте в очередной математической олимпиаде от Систематики! Олимпиада проходит в два тура, по итогам которых победители получают ценные призы грамоты и дипломы.
Зарегистрироваться
Бесплатно


