Задания 1-го тура XV олимпиады по математике для 3 класса

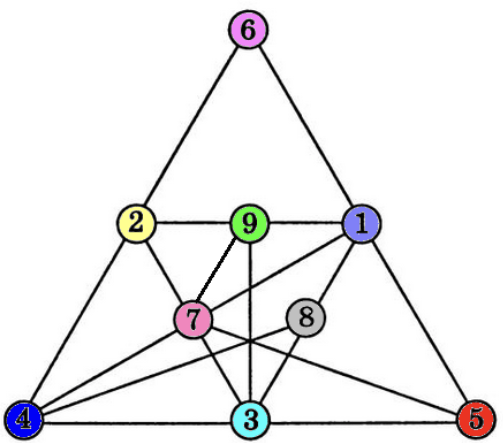
На картинке ниже цифрами обозначены люди: 1 — Егор; 2 — Лиза; 3 — Маша; 4 — Саша; 5 — Олег; 6 — Герман; 7 — Полина; 8 — Карина; 9 — Тимофей. Линии между цифрами показывают кто с кем дружит. Определите у кого больше всего друзей.

Вероника собирала бусы в подарок и располагала бусины в следующем порядке: синяя круглая, красная розочка, 2 зелёных лепесточка, синяя круглая, красная розочка, и так далее. Сколько синих бусин Веронике потребовалось для бус, если последняя бусина была синяя круглая и на бусы ушло 9 красных розочек?

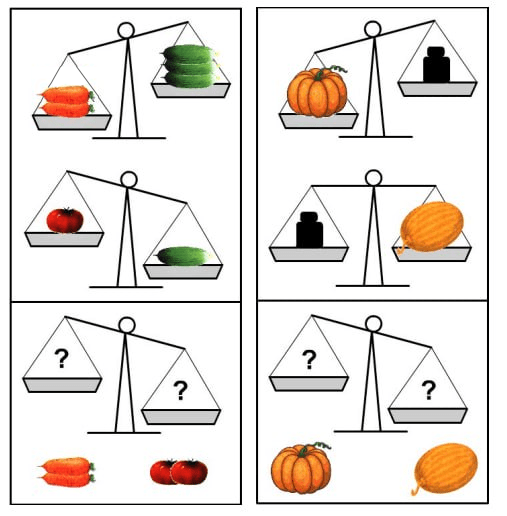
Что покажут весы?

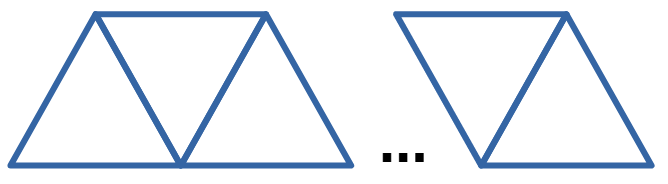
Петя из 21 спички сделал треугольник. Аня разобрала его и потратив все спички сложила полоску из треугольников. Сколько треугольников получилось?

Дядя Фёдор выкладывал из палочек римские числа по порядку от 1 до 11, причём что бы выложить I ему нужна одна спичка, а чтобы выложить V и X -- по две. Пришёл Шарик и убрал слева и справа по 14 палочек. Какое число осталось у Дяди Фёдора?

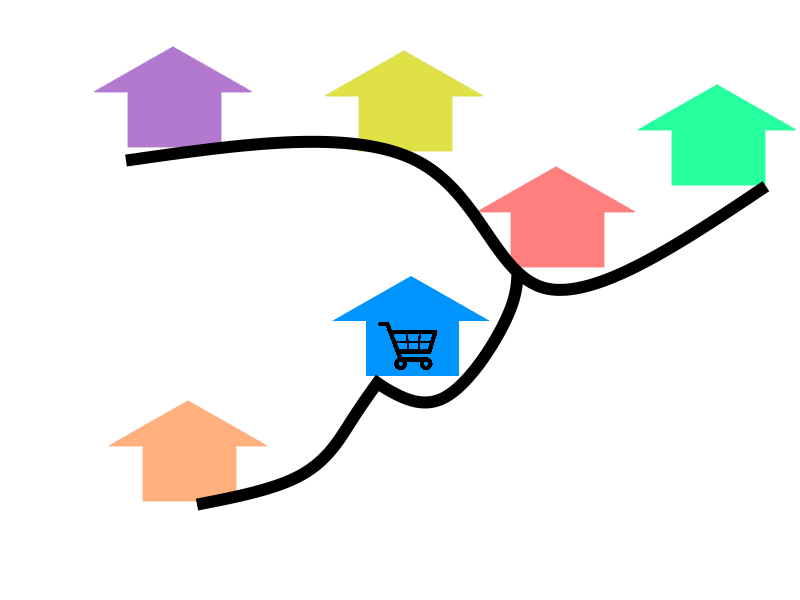
По дороге в магазин Маша прошла мимо дома Сережи. Из магазина она пошла в гости к Свете, попутно пройдя мимо своего дома. Где живет Света?

В четыре пробирки налита кислота. Высота каждой пробирки – 12 см. 1-й и 2-й стакан заполнены до отметки в 9 см, 3-й – до отметки в 10 см, 4-й – до отметки в 4 см. Грю хочет разлить кислоту так, чтобы во всех пробирках ее оказалось поровну. За один раз он может перелить кислоту из одной пробирки в другую так, чтобы вторая оказалась заполнена до краев, либо так, кислоты в пробирках стало поровну. За какое наименьшее количество шагов он может это сделать?

На паутине висело несколько существ - жуков и пауков. Чтобы раскрыть очень запутанное дело, Жак Клузо пересчитал головы и лапки всех существ. Оказалось, что лапок было 82, а голов 12. Помогите непревзойденному детективу раскрыть дело – выяснить сколько на паутине висело жуков.

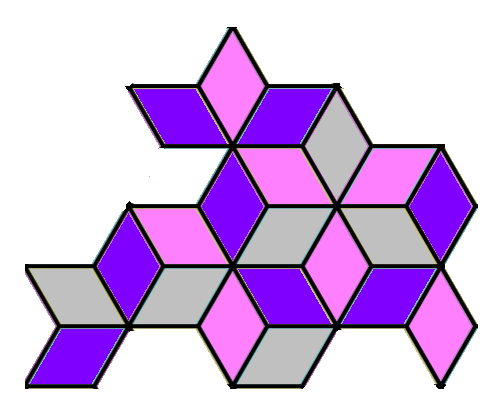
На сколько одинаковых фигурок можно разрезать фигурку нарисованную ниже. Части не могут состоять из 1 плиточки.

Фрекен Бок подарила Малышу шоколадку, разделённую бороздками на 6 × 8 маленьких плиточек. Карлсон предлагает Малышу сыграть в такую игру. Каждый по очереди разламывает любой из кусков по одной из бороздок (по прямой от края до края). Тот, после хода которого вся шоколадка будет разделена на отдельные плиточки, съедает всю шоколадку. Чтобы сходить первому, Карлсон предлагает делить шоколадку в следующей последовательности: Карлсон, Малыш, Фрекен Бок, Малыш, Карлсон, Малыш, Фрекен Бок, Малыш и т.д. Кто выиграет и съест шоколадку?