Задания 2-го тура XV олимпиады по математике для 8 класса
2 тур XV олимпиады по математике прошел 25 февраля 2024 года.
Задачи олимпиады
Задача №1
Сколькими способами можно представить 2024 в виде (a-b)*(a+b) где a и b - целые числа?
Иванюк Д. В.
Задача №2
В 2023 году почтовая марка первого класса стоила 85 центов, а почтовая марка второго класса — 66 центов. Какое наименьшее суммарное количество марок нужно приобрести, чтобы потратить целое количество долларов? (1 доллар = 100 центов).
Задача №3
Решить уравнение в целых числах:
Галиулина В. Н.
Задача №4
На схеме изображены два симметрично расположенных квадрата со сторонами 2 и 5. Каково отношение площади маленького квадрата к площади заштрихованной части?
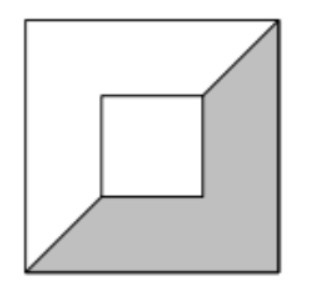
Задача №5
Двоечник Вася уже в начале ноября имел три двойки, четыре тройки, одну четверку и одну пятерку (за то, что выучил наизусть весь параграф по теме "среднее арифметическое натуральных чисел"). Воодушевившись текущим успехом, Вася решает получить пятерку по математике за всю вторую четверть, даже не смотря на свои предыдущие отметки. Сможет ли Вася добиться своей цели, если до конца четверти еще целых тридцать уроков по математике? (на одном уроке нельзя получить больше одной оценки, а пятерка за четверть выставляется только при среднем балле от 4.5).
Миронов Д. Р.
Задача №6
Согласно стандартам Союза европейских футбольных ассоциаций, размер футбольных ворот составляет: 7,32 метра в длину и 2,44 метра в высоту. Пенальти (штрафной удар) пробивается с белой метки, находящейся в 10,97 метра от линии ворот, на равном удалении от штанг ворот. Какое максимальное расстояние может преодолеть мяч до пересечения линии ворот, удар которым был нанесен с "точки пенальти", если будет двигаться только по прямой (размерами мяча, шириной штанг и перекладины можно пренебречь). Ответ округлите до сотых.
Миронов Д. Р.
Задача №7
Андрей заказал пиццу, которая согласно заявленным характеристикам, должна была быть 50 сантиметров в диаметре. Однако, произведя измерение готового продукта, Андрей заметил, что фактический размер пиццы составил 47 см в диаметре. Андрей был недоволен, и потребовал вернуть ему сумму денег, эквивалентную недостающей части пиццы. Какую сумму денег должны вернуть Андрею, если ее стоимость 1000 рублей? Ответ округлите до целого числа рублей.
Миронов Д. Р.
Задача №8
Верно ли, что для любого n>1 верно выражение:
Иванюк Д. В.
I тур: 15 сентября - 27 сентября 2026
II тур: 25 октября 2026
Олимпиада по математике
Двадцать первая международная
Участвуйте в очередной математической олимпиаде от Систематики! Олимпиада проходит в два тура, по итогам которых победители получают ценные призы грамоты и дипломы.
Регистрация участника
Бесплатно



