Задания 1-го тура XVI олимпиады по математике для 3 класса
1 тур XVI олимпиады по математике прошел с 25 сентября — 13 октября 2024 г
Задачи олимпиады
Задача №1
В вазе стояли пять цветов: астра, гербера, лилия, роза и тюльпан. Два цветка завяли. Какие пары могли завянуть? Укажи количество возможных вариантов.
(А) 10 (Б) 6 (В) 8 (Г) 9 (Д) 5
Задача №2
Между первым и вторым этажом два пролёта лестницы, каждый из которых по 15 ступенек. Ваня поднялся на последний этаж. Потом начал спускаться на первый, считая по пути ступеньки. Сколько этажей в доме, если Ваня насчитал 360 ступенек?
(А) 10 (Б) 12 (В) 13 (Г) 24 (Д) 25
Задача №3
В магазин привезли валенки: серого, бежевого и черного цветов разных размеров: 36, 38, 40. Все в одной коробке, причём есть по 3 пары валенок каждого из возможных сочетаний цвета и размера. Продавщица не успела разобрать коробку по парам, когда в магазин зашла бабушка и попросила померить черные валенки 36 размера. Валенки симметричные, подходят и на левую, и на правую ногу. Какое минимальное количество валенок должна будет достать продавщица из коробки не глядя, чтобы точно достать нужную пару?
(А) 2 шт (Б) 36 шт (В) 46 шт (Г) 50 шт (Д) 52 шт

Иванюк Е. В.
Задача №4
Фигуру, изображенную ниже, разрезали на 5 различных по площади прямоугольников по линиям сетки. Шаг сетки считать равным 1*1. Чему равен периметр прямоугольника с наибольшей площадью?
(А) 8 (Б) 10 (В) 12 (Г) 14 (Д) 16
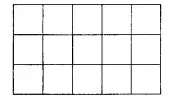
Галиулина В. Н.
Задача №5
Каждый день с утра многоножка идет на прогулку. Первые 20 пар своих ног она обувает за 40 минут. А на то, чтобы надеть обувь на ноги начиная с десятой пары, заканчивая последней, у нее уходит 32 минуты. Сколько ног у многоножки?
(А) 26 (Б) 40 (В) 42 (Г) 50 (Д) 52
Галиулина В. Н.
Задача №6
Три подруги в сумме набрали на экзамене по математике 265 баллов. Если бы Катя набрала на 12 баллов меньше, Рита — на 15 баллов меньше, а Лена — на 19 баллов меньше, то все они набрали бы поровну. Сколько баллов набрали Катя и Лена вместе?
(А) 73 (Б) 146 (В) 177 (Г) 85 (Д) 173
Задача №7
Сосчитайте сколько четырёхугольников в этой фигуре?
(А) 21 (Б) 20 (В) 19 (Г) 22 (Д) 15
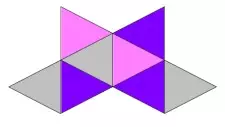
Иванюк Е. В.
Задача №8
Двое рабочих укладывают плитку. Первый: • выкладывает слева направо, начиная с нижнего ряда; • когда один ряд закончен, рабочий переходит на ряд выше, сохраняя направление работы. Второй: • выкладывает плитку сверху вниз, начиная с крайнего левого ряда; • когда один ряд закончен, рабочий переходит на ряд правее, сохраняя направление работы. Если плитка уже положена, то второй раз её не укладывают. Начинают они одновременно, работают с одинаковой скоростью. Какую плитку первый рабочий уложит последней?
(А) 1 (Б) 2 (В) 3 (Г) 4
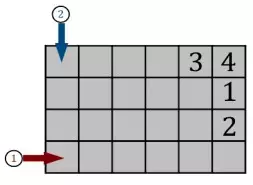
Галиулина В. Н.
Задача №9
Когда Том Сойер вернулся в свою хижину уже смеркалось, и он зажег свечку. Когда свечка прогорела на треть, он зажег вторую свечку. Когда вторая свечка прогорела на две третьих, он зажёг третью свечку. Сколько времени горели свечи, если каждая свечка полностью сгорает за 1 час 30 минут?
(А) 1 час 30 минут (Б) 3 часа (В) 2 часа 30 минут (Г) 2 часа (Д) 1 час
Иванюк Е. В.
Задача №10
У Мухи-Цокотухи множество дочерей и сыновей. Однажды, она открыла коробку конфет и разрешила всем мушатам взять по 3 конфетки. От сладкого у детишек заболели животы, поэтому, на следующий день, когда она открыла такую же коробку конфет, она разрешила всем брать только по одной конфетке. Сколько детей у Цокотухи, если в первый день в коробке осталось всего одна конфета, а во второй – 31?
(А) 10 (Б) 15 (В) 16 (Г) 30 (Д) 32
| Задача № | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Ответ | А | В | Г | В | Г | В | А | А | Б | Б |
I тур: 15 сентября - 27 сентября 2026
II тур: 25 октября 2026
Олимпиада по математике
Двадцать первая международная
Участвуйте в очередной математической олимпиаде от Систематики! Олимпиада проходит в два тура, по итогам которых победители получают ценные призы грамоты и дипломы.
Регистрация участника
Бесплатно



