Дарим курс
Математика: перезагрузка
Задания 1-го тура XVII олимпиады по математике для 1 класса
Именные сертификаты и призы
2 тура: онлайн и очно
Для учеников 1–9 классов
Скидка действует только до 23:59 сегодня. Успейте воспользоваться!
1 тур XVII олимпиады по математике прошел с 21 января по 9 февраля 2025 года.
Задача №1
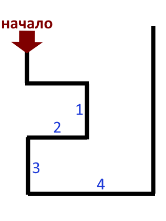
Краб Себастьян полз по дорожке. Потом развернулся спиной вперед и так и прополз до самого конца. По пути он подсчитал, что на поворотах дороги один раз сворачивал налево и пять раз направо. На каком участке дорожки он развернулся спиной?
А) 1 Б) 2 В) 3 Г) 4
Галиулина В. Н.
Задача №2
За один ход можно выбрать любую букву в слове и переместить её в начало. За какое наименьшее число ходов можно из ВОЛОС получить СЛОВО?
А) 2 Б) 3 В) 4 Г) 5
Галиулина В. Н.
Задача №3
Собака на 10 килограмм тяжелее двух кошек, а кошка на 4 килограмма тяжелее крысы. Насколько собака тяжелее двух крыс?
А) 28 Б) 16 В) 12 Г) 18
Галиулина В. Н.
Задача №4
У Аркаши-фокусника есть три коробки. В каждой лежит картонная фигура — квадрат, треугольник или круг. Известно, что круг лежит не в первой коробке, во второй коробке лежит не квадрат, треугольник лежит либо в первой, либо во второй коробке. Аркаша открыл первую коробку, и достал из нее фигуру, на нее он положил фигуру из второй коробки, а сверху — фигуру из третьей коробки. Что у него могло получиться в результате?
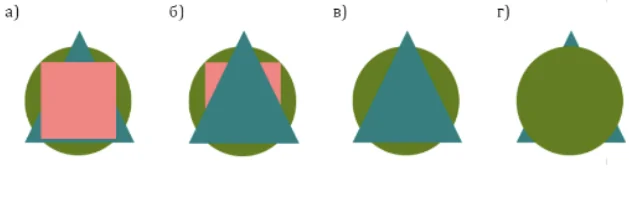
Галиулина В. Н.
Задача №5
Шестиугольную звезду согнули пополам (так, что две половинки совместились), затем, еще раз пополам, снова совместив половинки. Какой результат мог получиться после того, как звезду развернули?
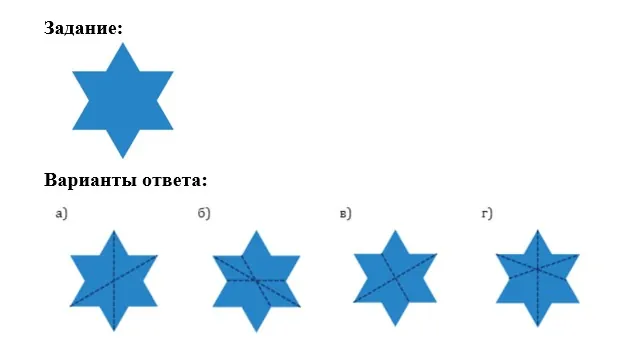
Галиулина В. Н.
Задача №6
У Никиты, Нади и Жени вместе 22 конфеты. Известно, что у Никиты и Нади вместе 12 конфет, а у Нади и Жени вместе 17 конфет. Сколько конфет у Нади?
А) 5 Б) 6 В) 7 Г) 10
Родин Р. В.
Задача №7
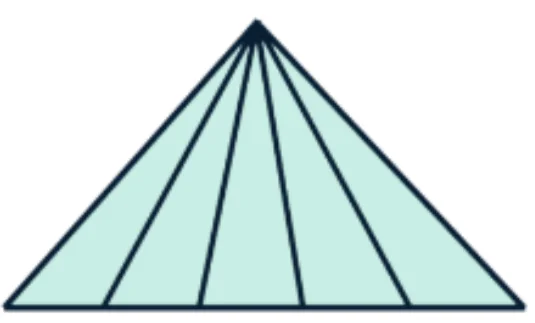
Сколько треугольников в фигуре на картинке?
А) 9 Б) 6 В) 15 Г) 5 Д) 12
Галиулина В. Н.
Задача №8
У Лены есть четыре обруча: красный, зелёный, синий и жёлтый. Красный может пролезть ровно в один из двух обручей — зелёный или синий. В жёлтый обруч пролезает ровно один обруч, а синий обруч не пролезет сквозь жёлтый. Какой обруч самый маленький?
А) красный Б) зелёный В) синий Г) жёлтый
Галиулина В. Н.
Задача №9
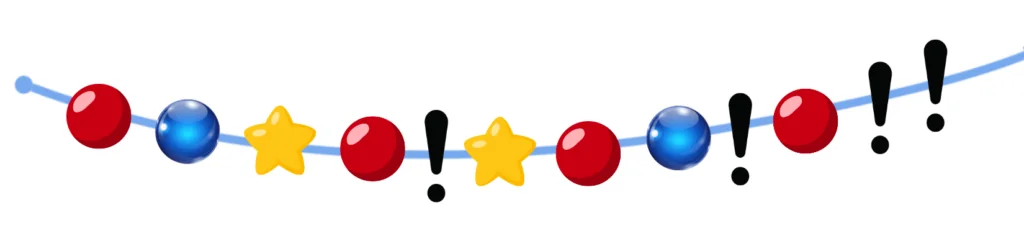
Фея хочет собрать красивое ожерелье. Для этого она нанизывает на нитку бусинки в одном и том же порядке. Некоторые бусинки спрятаны за знаками "!". Какая бусинка находится на месте последнего знака "!"?
А) красный кружок Б) синий кружок В) жёлтая звёздочка Г) нельзя определить
Родин Р. В.
Задача №10
На опушке Сказочного леса стоят три домика: красный, синий и зелёный. В них живут белка, заяц и лица. Причём:
● Белка не живет в красном домике;
● Заяц живет не в синем и не в зелёном домике;
● Лиса не живет в зелёном домике.
Кто в каком домике живёт?
● Белка не живет в красном домике;
● Заяц живет не в синем и не в зелёном домике;
● Лиса не живет в зелёном домике.
Кто в каком домике живёт?
А) белка в красном, заяц в синем, лиса в зелёном Б) белка в синем, заяц в зелёном, лиса в красном В) белка в зелёном, заяц в красном, лиса в синем Г) белка в синем, заяц в красном, лиса в зелёном
Родин Р. В.
| Задача № | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Ответ | Б | Б | Г | Г | В | В | В | Б | В | В |
Пробная олимпиада
Пройдите пробную олимпиаду по математике для 1–9 классов.
1-й тур: 16 – 29 июня
2-й тур: 20 июля
Олимпиада по математике
Восемнадцатая международная олимпиада по математике
Участвуйте в очередной математической олимпиаде от Систематики! Олимпиада проходит в два тура, по итогам которых победители получают ценные призы грамоты и дипломы.
Именные сертификаты и призы
2 тура: онлайн и очно
Для учеников 1–9 классов
Зарегистрироваться
Бесплатно