Задания 1-го тура XVII олимпиады по математике для 2 класса
1 тур XVII олимпиады по математике прошел с 21 января по 9 февраля 2025 года.
Задачи олимпиады
Задача №1
У Лены есть четыре обруча: красный, зелёный, синий и жёлтый. Красный может пролезть ровно в один из двух обручей — зелёный или синий. В жёлтый обруч пролезает ровно один обруч, а синий обруч не пролезет сквозь жёлтый. Какой обруч самый маленький?
А) красный Б) зелёный В) синий Г) жёлтый
Галиулина В. Н.
Задача №2
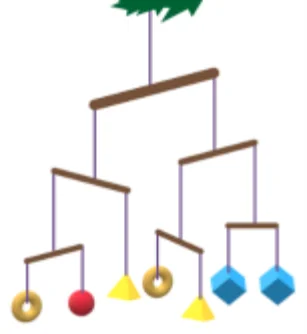
Расставьте ёлочные украшения от самого лёгкого к самому тяжёлому.
А) Сушка, шарик, пирамидка, кубик Б) Шарик, сушка, кубик, пирамидка В) Кубик, шарик, сушка, пирамидка Г) Шарик, кубик, сушка пирамидка
Галиулина В. Н.
Задача №3
На блюде лежало 20 эклеров. После того, как несколько штук съела Шарлотта, Тиана взяла на 3 меньше. Сколько осталось эклеров, если известно, что их осталось на 5 больше, чем взяла Тиана?
А) 9 Б) 5 В) 6 Г) 11
Галиулина В. Н.
Задача №4
У Аркаши-фокусника есть три коробки. В каждой лежит картонная фигура – квадрат, треугольник или круг. Известно, что круг лежит не в первой коробке, во второй коробке лежит не квадрат, треугольник лежит либо в первой, либо во второй коробке. Аркаша открыл первую коробку, и достал из нее фигуру, на нее он положил фигуру из второй коробки, а сверху – фигуру из третьей коробке. Что у него могло получиться в результате?
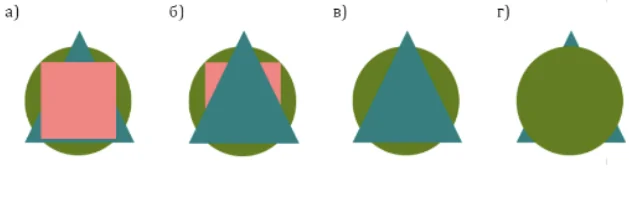
Галиулина В. Н.
Задача №5
Когда Алиса попала в Страну Чудес, ей рассказали, что, если погладить мюмзика по пузику, он начнет урчать. Если мюмзик заурчит, то молоко поблизости скиснет. Выберите точно верное утверждение.
А) если не погладить мюмзика по пузику, то молоко поблизости не скиснет; Б) если погладить мюмзика по пузику, молоко поблизости скиснет; В) если поставить молоко далеко, то оно не точно скисает от поглаживаний мюмзика Г) есть несколько верных ответов
Галиулина В. Н.
Задача №6
Чебурашка почистил 3 апельсина и разломал каждый из них пополам. Затем каждую половинку он разломил на дольки. Всего у него получилось 35 долек. Сколько разломов он сделал?
А) 35 Б) 38 В) 34 Г) 32
Галиулина В. Н.
Задача №7
Мама дала Маргоше восемь монеток, каждая из которых была по 2 или 5 рублей. Когда Маргоша пересчитала монетки, оказалось, что пятирублёвых монеток больше, чем двухрублёвых, и что все эти монетки вместе стоят 34 рубля. Сколько пятирублёвых монеток мама дала Маргоше?
А) 4 Б) 5 В) 6 Г) 7 Д) 8
Тодоров Е. И.
Задача №8
За один ход можно выбрать любую букву в слове и переместить её в начало. За какое наименьшее число ходов можно из ВОЛОС получить СЛОВО?
А) 2 Б) 3 В) 4 Г) 5
Галиулина В. Н.
Задача №9
Шестиугольную звезду согнули пополам (так, что две половинки совместились!), затем, еще раз пополам, снова совместив половинки. Какой результат мог получиться после того, как звезду развернули?
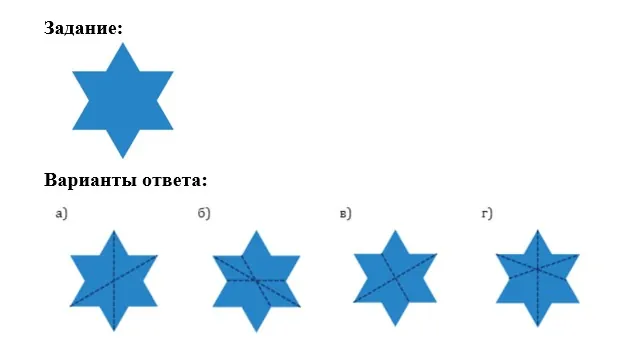
Галиулина В. Н.
Задача №10
У Миши, Даши и Кати есть конфеты. У Миши и Даши вместе 8 конфет. У Даши и Кати вместе 7 конфет. У Миши и Кати вместе 9 конфет. Сколько конфет у Кати?
А) 3 Б) 4 В) 5 Г) 6
Родин Р. В.
| Задача № | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Ответ | Б | В | А | Г | Б | Г | В | Б | В | Б |
I тур: 15 сентября - 27 сентября 2026
II тур: 25 октября 2026
Олимпиада по математике
Двадцать первая международная
Участвуйте в очередной математической олимпиаде от Систематики! Олимпиада проходит в два тура, по итогам которых победители получают ценные призы грамоты и дипломы.
Регистрация участника
Бесплатно


