Задания 2-го тура XVII олимпиады по математике для 2 класса
2 тур XVII олимпиады по математике прошел 2 марта 2025 года.
Задачи олимпиады
Задача №1
На полянке собралась весёлая компания из 23 букашек – жучков, паучков и червячков. У каждого жучка 6 ножек и нет хвостика, у каждого паучка 8 ножек и нет хвостика, а у каждого червячка нет ножек, но есть хвостик. Сколько жучков приползло на полянку, если оказалось, что количество лапок равно количеству хвостов? Ответ объясните.

Галиулина В. Н.
Задача №2
«Можете ли вы сказать мне, какая температура была в полдень в течение последних пяти дней?» — спросил Сергей у синоптика. «Я точно не помню», — ответил синоптик. «Но я помню, что каждый день становилось на 1 градус теплее, чем было в прошлый день, и что сумма температур была равна 25». Какими были эти пять температур?
Иванюк Е. В.
Задача №3
Шестерёнку “1” хотят повернуть по часовой стрелке. Повернутся ли другие шестерёнки? Ответ объясните
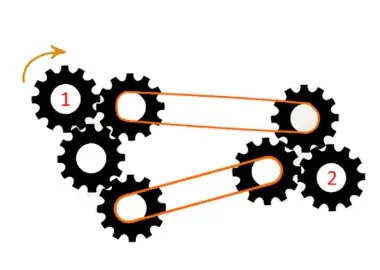
Галиулина В. Н.
Задача №4
Петя взял прямоугольник размера 6 x 10, вырезал из него два прямоугольника 2 x 4 и получил фигурку в форме буквы “Н” (см. рисунок). Теперь Петя хочет заполнить эту фигурку плитками 1 x 1, которые продаются только в коробках по 6 штук. Какое наименьшее количество коробок с плиткой необходимо купить, чтобы выложить «H»?

Галиулина В. Н.
Задача №5
У пирата Чёрной Бороды есть сундук с сокровищами. В нём лежат: 12 золотых монет, 7 серебряных монет, 3 жемчужины. Чёрная Борода решил разделить Сокровища между своими тремя помощниками. Сначала он разделил золотые монеты поровну, затем разделил серебряные монеты поровну, остатки отложил в сторону. После этого он взял жемчужины и разделил их поровну между помощниками. Сколько монет и жемчужин осталось у чёрной бороды?
Родин Р. В.
Задача №6
Узор сделан из 25 маленьких плиток. Плитки, которые получаются одна из другой поворотом или отражением считаются одинаковыми. Сколько всего существует видов плиток? Ответ объясните.
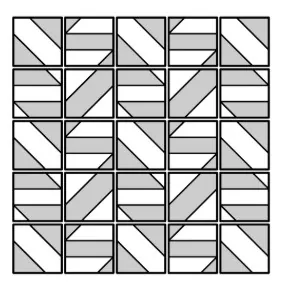
Галиулина В. Н.
Задача №7
Сейчас счетчик мандаринов, съеденных Павликом, показывает 5125. В этом числе цифра 5 встречается дважды. Какое минимальное количество мандаринов нужно съесть Павлику, чтобы на его счетчике вновь оказались две одинаковые цифры? Ответ объясните.
Галиулина В. Н.
Задача №8
На клетчатом листе бумаги нарисованы цифры 3, 4 и 5 так, как показано на рисунке: Цифра 3 сама по себе симметрична, то есть её можно разделить красной линией на две зеркальные половинки, как показано на втором рисунке: Соберите из цифр 3, 4 и 5, взятых по одному разу, картинку, которую тоже можно было бы разделить линией на две симметричные половинки. Цифры можно класть на бок.

Тодоров Е. И.
I тур: 15 сентября - 27 сентября 2026
II тур: 25 октября 2026
Олимпиада по математике
Двадцать первая международная
Участвуйте в очередной математической олимпиаде от Систематики! Олимпиада проходит в два тура, по итогам которых победители получают ценные призы грамоты и дипломы.
Регистрация участника
Бесплатно



