Пробная олимпиада
Задания 1-го тура XVIII олимпиады по математике для 1 класса
Именные сертификаты и призы
2 тура: онлайн и очно
Для учеников 1–9 классов
1 тур XVII олимпиады по математике прошел с 16 по 19 июня 2025 года.
Задача №1
В паутине запутались 7 мух, на пир пришло два паучка, которые очень быстро проглотили целиком 2 мухи. Сколько лап сейчас в паутине? (У всех мух по 6 лапок, а у паучков - по 8)
А) 42 Б) 46 В) 48 Г) 50
Галиулина В. Н.
Задача №2
В семействе семь гномов. Фалин старше Троила, но младше Балина. Троил не самый молодой, а Гимли самый старший. Фили старше Кили, а Кили старше Фалина. А какой по старшинству седьмой брат — Горин?
А) Самый молодой Б) Второй по старшинству В) Средний по возрасту Г) Невозможно однозначно определить
Галиулина В. Н.
Задача №3
Выберите из предложенных вариантов фигуру, которая точно подходит в качестве одной из частей рисунка. Поворачивать и отражать фигурки нельзя.
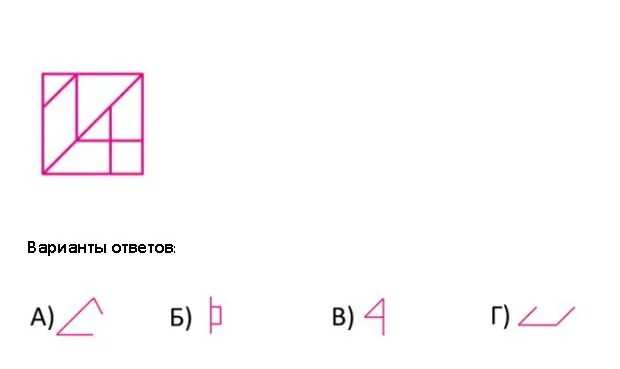
Галиулина В. Н.
Задача №4
Женя и Света живут в одном доме, но Женя считает этажи дома снизу вверх, а Света — сверху вниз. Как-то раз они гуляли около дома, и Женя сказал: — Я живу на втором этаже. А ты — на четвёртом. — Нет, это я живу на втором этаже, — ответила Света. — А ты — на четвёртом. Сколько этажей в их доме?
А) 4 Б) 5 В) 6 Г) 7
Тодоров Е.И.
Задача №5
Каждый месяц купец Семён получает зарплату и откладывает в копилку 2, 3 или 5 рублей. Какую из перечисленных сумм он не мог накопить за 6 месяцев?
А) 15 Б) 27 В) 28 Г) 29
Тодоров Е.И.
Задача №6
На какой веревочке завяжется узелок, если потянуть её за концы?
А) 1 Б) 2 В) 3 Г) 4
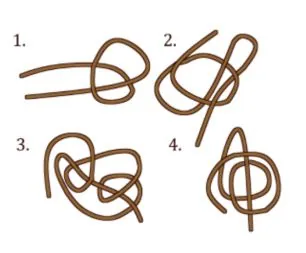
Галиулина В. Н.
Задача №7
Ира решила испечь 10 пирогов, каждый из которых нужно выпекать в духовке в течение 19 минут. В духовку одновременно помещается только 2 пирога. Первую пару она поставила в духовку в 11:40. Как только пара испечена, Ира тут же достаёт её из духовки и ставит новую. Во сколько испечется последняя пара?
A) 12:15 Б) 12:40 В) 13:15 Г) 14:15
Галиулина В. Н.
Задача №8
Каждое число в верхних строчках пирамидки получается из чисел ниже одним и тем же способом. Определите, что это за способ. Какое число стоит в вершине пирамидки на месте буквы х?
A) 100 Б) 82 В) 55 Г) 50
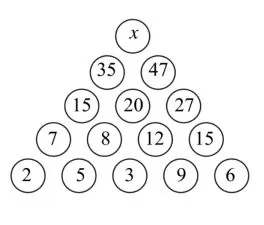
Галиулина В. Н.
Задача №9
Целый квадратный лист бумаги сложили пополам два раза так, что получился квадрат меньшего размера. Затем от него отрезали уголок, как показано на рисунке. Что могло получиться, когда квадрат развернули?
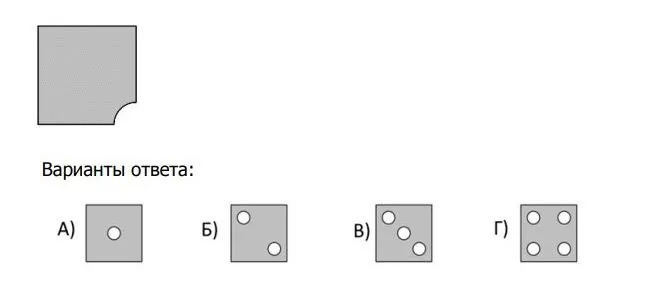
Галиулина В. Н.
Задача №10
На участке было посажено 54 берёзы и не было кустов. Каждое утро сажают один смородиновый куст, а одну из берёз срубают. Через сколько дней кустов будет ровно в два раза больше, чем берёз?
А) 33 Б) 36 В) 39 Г) 40
Тодоров Е.И.
| Задача № | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Ответ | Б | А | В | Б | Г | В | В | Б | А | Б |
Пройдите пробную олимпиаду по математике для 1–9 классов.
1-й тур: 15 – 29 сентября
2-й тур: 20 июля
Олимпиада по математике
Девятнадцатая международная олимпиада по математике
Участвуйте в очередной математической олимпиаде от Систематики! Олимпиада проходит в два тура, по итогам которых победители получают ценные призы грамоты и дипломы.
Именные сертификаты и призы
2 тура: онлайн и очно
Для учеников 1–9 классов
Зарегистрироваться
Бесплатно