Пробная олимпиада
Задания 1-го тура XVIII олимпиады по математике для 2 класса
Именные сертификаты и призы
2 тура: онлайн и очно
Для учеников 1–9 классов
1 тур XVIII олимпиады по математике прошел с 16 по 29 июня 2025 года.
Задача №1
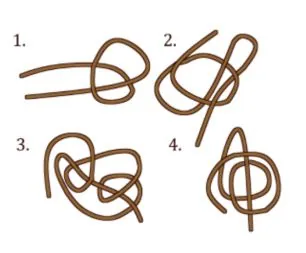
На какой веревочке завяжется узелок, если потянуть её за концы?
А) 1 Б) 2 В) 3 Г) 4
Галиулина В. Н.
Задача №2
На чаепитии в качестве гостей присутствовали пять рыцарей и три принцессы. Королева подметила, что среди гостей трое были со светлыми волосами, а пятеро — с тёмными. Кто точно присутствовал на чаепитии?
А) Светловолосая принцесса Б) Светловолосый рыцарь В) Темноволосый рыцарь Г) Темноволосая принцесса
Галиулина В. Н.
Задача №3
В семействе семь гномов. Фалин старше Троила, но младше Балина. Троил не самый молодой, а Гимли самый старший. Фили старше Кили, а Кили старше Фалина. А какой по старшинству седьмой брат — Горин?
А) Самый молодой Б) Второй по старшинству В) Средний по возрасту Г) Невозможно однозначно определить
Галиулина В. Н.
Задача №4
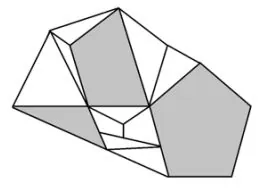
Арсений нарисовал фигуру и раскрасил некоторые из её частей серым цветом (см. рис.). Теперь он хочет раскрасить остальные её части в какие-то другие цвета так, чтобы две части одного цвета не соприкасались по стороне. Какое наименьшее число других цветов ему для этого необходимо?
А) 1 Б) 2 В) 3 Г) 4
Галиулина В. Н.
Задача №5
На участке посажено 102 берёзы и нет кустов. Каждое утро сажают один смородиновый куст, а одну из берез срубают. Через сколько дней кустов будет ровно в два раза больше, чем берёз?
А) 50 Б) 64 В) 66 Г) 68
Галиулина В. Н.
Задача №6
Каждый месяц, когда богатый Сэм получает зарплату, он откладывает в копилку 2, 3 или 5 рублей. Какую из перечисленных сумм он не мог накопить за год?
А) 33 Б) 43 В) 57 Г) 59
Галиулина В. Н.
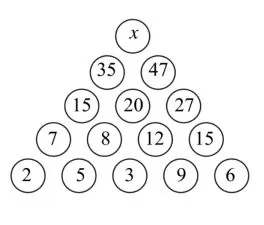
Задача №7
A) 100 Б) 82 В) 55 Г) 50
Галиулина В. Н.
Задача №8
В замке злого короля есть 50 камер с номерами от 1 до 50. В каждой камере сидит в два раза больше заключённых, чем номер этой камеры. Каждую камеру охраняют стражники. Первую — 1 стражник, вторую — 3 стражника, третью — 5 и так далее. На сколько заключенных больше, чем стражников?
A) 50 Б) 100 В) 255 Г) 125
Галиулина В. Н.
Задача №9
В волшебном лесу эльфу нужно добраться до подснежника, прыгая по пенькам. Он начинает с пенька №1 и должен закончить на пеньке №5, прыгая каждый раз на соседний пенёк с большим номером. Сколько существует возможных маршрутов для эльфа, чтобы добраться до подснежника?
A) 7 Б) 5 В) 6 Г) 11
Галиулина В. Н.
Задача №10
Алмазные подвески были похищены. В центре разбирательства оказались четверо друзей: Арина, Серёжа, Игорь и Лёша. Арина уверенно заявила, что Игорь невиновен; Сережа обвинил Лёшу; Игорь сказал, что преступником был Серёжа; Лёша защитил Арину, говоря, что она не могла быть причастна к преступлению. Лжёт только виновный, все остальные говорят правду. Кто на самом деле виновен?
A) Арина Б) Игорь В) Серёжа Г) Лёша
Галиулина В. Н.
| Задача № | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Ответ | В | В | А | В | Г | Г | Б | А | Б | В |
Пройдите пробную олимпиаду по математике для 1–9 классов.
1-й тур: 15 – 29 сентября
2-й тур: 20 июля
Олимпиада по математике
Девятнадцатая международная олимпиада по математике
Участвуйте в очередной математической олимпиаде от Систематики! Олимпиада проходит в два тура, по итогам которых победители получают ценные призы грамоты и дипломы.
Именные сертификаты и призы
2 тура: онлайн и очно
Для учеников 1–9 классов
Зарегистрироваться
Бесплатно