Задания 1-го тура XVIII олимпиады по математике для 4 класса

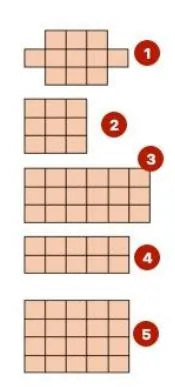
Марьяна испекла 5 венских вафель (СМ рис). Её брат Андрей успел съесть 4 вафли целиком, потратив на всё целое число секунд. Самую большую вафлю он съел за 4 секунды, каждую клеточку вафли он ест с одной и той же скоростью. Какую вафлю он не успел съесть?

В королевстве Кривых Зеркал, собрались четверо друзей; некоторые из них всегда говорят правду, а остальные всегда лгут. В один из вечеров они решили проверить свои способности, заявив о количестве правдивых людей в их компании: Первый сказал: “Нечетное число из нас всегда говорит правду”. Второй сказал: “Четное число из нас всегда говорит правду”. Третий сказал: “Простое число из нас всегда говорит правду”. Четвертый сказал: “Число тех, кто всегда говорит правду - это квадрат какого-то числа”. Сколько из четырех друзей говорили правду?

Мама дала Катеньке несколько монеток по 2 и 5 рублей, причём точно были и такие, и такие. Сколькими различными способами мама могла так дать монетки Катеньке, чтобы пятирублёвых монеток было не больше, чем двухрублёвых, и чтобы все эти монетки вместе стоили 42 рубля?

В детском саду Ромашка меньше 500 воспитанников. Пятая часть от всех ребят сегодня не съела суп на обед, четверть — не выпила компот, треть — отказалась от котлеты, а одна седьмая — отдала кусочек хлеба соседу. Сколько ребят не выпили компот?

В трех банках сидят долгоносики: в первой банке 16, во второй — 28, а в третьей — 37. Каждую минуту один долгоносик переползает из одной банки в любую другую. Найдите минимальное время, спустя которое могло оказаться, что во всех банках долгоносиков поровну.

На отрезке AD длиной 48 сантиметров стоят точки B и C так, что: точки расположены в порядке ABCD; отрезок AC в шесть раз длиннее отрезка AB; а отрезок CD — в 3 раза короче AC. Найдите длину отрезка BD.

Лизе очень скучно, поэтому она делает с числом n одно из следующих действий: – если n<5, Лиза умножает его на 4 – если число n>=5 и чётное, Лиза делит его на 2 – если число n>=5 и нечётное, Лиза прибавляет к нему 3 Что получится, если Лиза применит 2025 таких действий к числу 7?

У Лизы есть очень тонкий лист бумаги размером 20х30 см. Она многократно складывает его пополам вдоль более короткой стороны. Она прекращает складывать, когда у нее остается прямоугольник площадью 75 см². Какой периметр у получившегося прямоугольника?

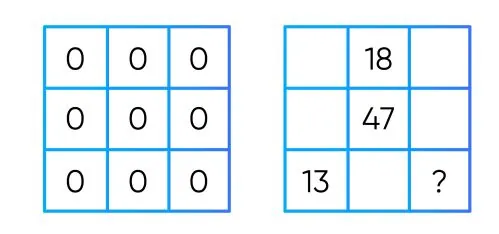
Учитель Марка нарисовал на доске сетку размером 3∗3, с нулем в каждой ячейке. Затем ученики по очереди выбирали квадрат размером 2∗2 и добавляли 1 к каждому из чисел в четырех ячейках. Через некоторое время сетка стала выглядеть как на рисунке справа (часть чисел в ячейках стерлась). Какое число должно быть в ячейке со знаком вопроса?

Каждую клетку полоски 1х2025 покрасили в красный, синий или зелёный цвет. Оказалось, что среди любых четырёх подряд идущих клеток есть ровно две красные, одна зелёная и одна синяя. Петя подглядел, что 7-ая клетка — синяя, а 8-ая — зелёная. Какого цвета 2025-ая клетка?